Page 141 - Fundamentals of Ocean Renewable Energy Generating Electricity From The Sea

132 Fundamentals of Ocean Renewable Energy

2
2
approaches ω N , the denominator becomes smaller (ω − ω → 0), and this
N F
leads to a larger response amplitude. Also, a larger damping coefficient leads to
an increase of the denominator or smaller amplitude.
To perform a more quantitative analysis, let us reformulate the amplitude in
√
Eq. (5.59) as follows (by replacing c d = 2ζ km,Eq. (5.56),
Fa/k s
= Fa/k s × (5.60)
z 1 =
2 2
ω F 2 ω F
1 − + 2ζ
ω N ω N
The numerator of the previous equation (Fa/k s ) is constant, but the denominator
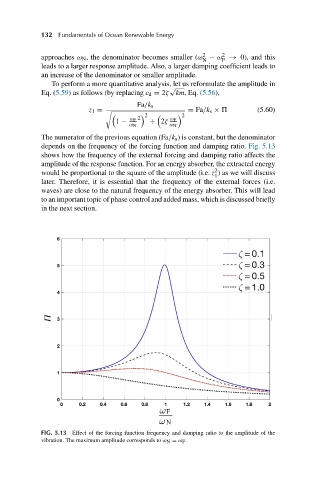
depends on the frequency of the forcing function and damping ratio. Fig. 5.13
shows how the frequency of the external forcing and damping ratio affects the
amplitude of the response function. For an energy absorber, the extracted energy
2
would be proportional to the square of the amplitude (i.e. z ) as we will discuss
1
later. Therefore, it is essential that the frequency of the external forces (i.e.
waves) are close to the natural frequency of the energy absorber. This will lead
to an important topic of phase control and added mass, which is discussed briefly
in the next section.

FIG. 5.13 Effect of the forcing function frequency and damping ratio to the amplitude of the
vibration. The maximum amplitude corresponds to ω N = ω F .