Page 139 - Fundamentals of Ocean Renewable Energy Generating Electricity From The Sea

130 Fundamentals of Ocean Renewable Energy

k s iω N t
= i =iω N →z=z o e or using the Euler’s formula z=z o cos(ω N t+g o )
m
(5.55)
√
where i = −1 and ω N = k is the natural frequency of the system. This is
m
equivalent to having a WEC in a calm sea with no damping. When it is displaced
from the equilibrium position, the system oscillates indefinitely. The solution for
an undamped system is a simple harmonic equation (i.e. z = z o cos(ω N t + g o )),
where the amplitude (z o ) and phase (g o ) of this harmonic motion depend on the
initial condition.
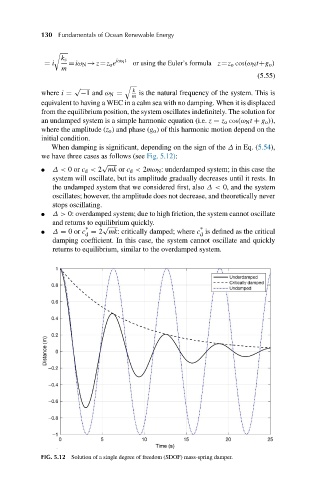
When damping is significant, depending on the sign of the Δ in Eq. (5.54),
we have three cases as follows (see Fig. 5.12):
√
● Δ< 0or c d < 2 mk or c d < 2mω N : underdamped system; in this case the
system will oscillate, but its amplitude gradually decreases until it rests. In
the undamped system that we considered first, also Δ< 0, and the system
oscillates; however, the amplitude does not decrease, and theoretically never
stops oscillating.
● Δ> 0: overdamped system; due to high friction, the system cannot oscillate
and returns to equilibrium quickly.
√
*
*
● Δ = 0or c = 2 mk: critically damped; where c is defined as the critical
d d
damping coefficient. In this case, the system cannot oscillate and quickly
returns to equilibrium, similar to the overdamped system.

FIG. 5.12 Solution of a single degree of freedom (SDOF) mass-spring damper.