Page 219 - Fundamentals of Ocean Renewable Energy Generating Electricity From The Sea

208 Fundamentals of Ocean Renewable Energy

Alternatively, conservation laws can be expressed by integral equations (i.e.
Reynolds transport theorem). For instance, the differential form of the continuity
equation can be written as
∂ρ ∂(ρu) ∂(ρv) ∂(ρw)
+ + + = 0 (8.27)
∂t ∂x ∂y ∂z
where u, v, and w are the components of flow velocities in the x, y, and z
directions, and ρ is the density. The integral form of continuity for a control
volume (or a finite volume) can be written as
∂
ρdV + ρu · dS = 0 (8.28)
∂t V S
where V is the control volume, S is the control surface, u = (u, v, w), and S is
the surface vector.
Therefore, the change of mass inside a control/finite volume plus the net
mass fluxes through the control surface should be zero. In FVM, the domain
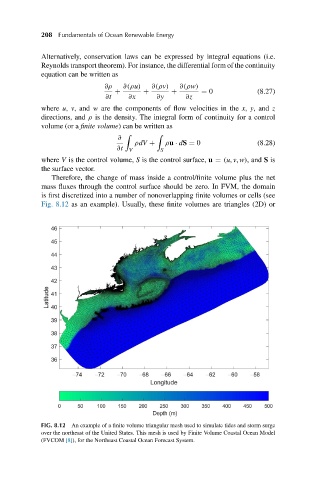
is first discretized into a number of nonoverlapping finite volumes or cells (see
Fig. 8.12 as an example). Usually, these finite volumes are triangles (2D) or

FIG. 8.12 An example of a finite volume triangular mesh used to simulate tides and storm surge
over the northeast of the United States. This mesh is used by Finite Volume Coastal Ocean Model
(FVCOM [8]), for the Northeast Coastal Ocean Forecast System.