Page 214 - Fundamentals of Ocean Renewable Energy Generating Electricity From The Sea

Ocean Modelling for Resource Characterization Chapter | 8 203

Another form is the central difference and, as shall be shown in the next
section on truncation error, it is more accurate than either backward or forward
difference. It is defined as

u(x i+1 + Δx) − u(x i − Δx) u(x i+1 ) − u(x i−1 ) u(x i+1 )−u(x i−1 )
du
= =
dx 2Δx 2Δx x i+1 −x i−1
x=x i
(8.10)
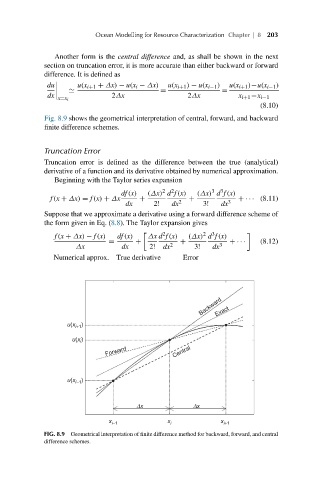
Fig. 8.9 shows the geometrical interpretation of central, forward, and backward
finite difference schemes.

Truncation Error
Truncation error is defined as the difference between the true (analytical)
derivative of a function and its derivative obtained by numerical approximation.
Beginning with the Taylor series expansion
2
3
2
3
df(x) (Δx) d f(x) (Δx) d f(x)
f(x + Δx) = f(x) + Δx + + + ··· (8.11)
dx 2! dx 2 3! dx 3
Suppose that we approximate a derivative using a forward difference scheme of
the form given in Eq. (8.8). The Taylor expansion gives
2
3
2
f(x + Δx) − f(x) df(x) Δx d f(x) (Δx) d f(x)
= + + + ··· (8.12)
Δx dx 2! dx 2 3! dx 3
Numerical approx. True derivative Error

Backward Exact

u(x )
i+1
u(x ) i
Forward Central

)
u(x i−1

Dx Dx
x i−1 x i x i+1

FIG. 8.9 Geometrical interpretation of finite difference method for backward, forward, and central
difference schemes.