Page 93 - Fundamentals of Physical Volcanology

9780632054435_4_005.qxd 12/10/2007 12:20PM Page 70

70 CHAPTER 5

0 bubbles are always trying to rise through the over-
lying magma even as the magma itself rises. The
buoyancy force which causes the bubbles to rise
through the magma is counteracted by the drag
force of friction exerted on the bubble as it moves
through the magma. As long as bubbles do not rise
Depth (m) as: B
100
too quickly they maintain a very nearly spherical
shape and so the buoyancy force, F , can be defined

3
F = (4/3) π r (ρ − ρ ) g (5.10)
B m g
200
where r is the bubble radius, and ρ and ρ are the
m g
magma and gas densities, respectively. As long as
10 10 2 10 3 10 4 the bubble radius does not become extremely big,
the drag force, F , is controlled just by the viscosity
Bubble radius (mm) D
of the magma, η, and is given by:
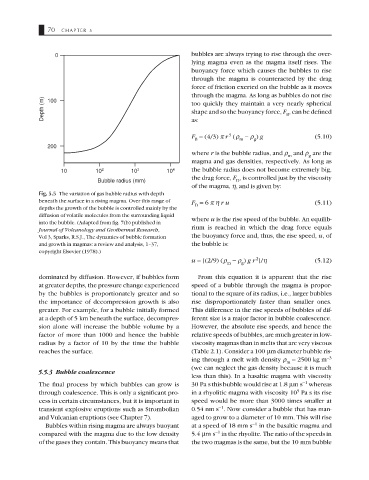
Fig. 5.5 The variation of gas bubble radius with depth
beneath the surface in a rising magma. Over this range of F = 6 πη ru (5.11)
depths the growth of the bubble is controlled mainly by the D
diffusion of volatile molecules from the surrounding liquid
where u is the rise speed of the bubble. An equilib-
into the bubble. (Adapted from fig. 7(b) published in
rium is reached in which the drag force equals
Journal of Volcanology and Geothermal Research,
Vol 3, Sparks, R.S.J., The dynamics of bubble formation the buoyancy force and, thus, the rise speed, u, of
and growth in magmas: a review and analysis, 1–37, the bubble is:
copyright Elsevier (1978).)
u = [(2/9) (ρ − ρ ) gr ]/η (5.12)
2
m g
dominated by diffusion. However, if bubbles form From this equation it is apparent that the rise
at greater depths, the pressure change experienced speed of a bubble through the magma is propor-
by the bubbles is proportionately greater and so tional to the square of its radius, i.e., larger bubbles

the importance of decompression growth is also rise disproportionately faster than smaller ones.
greater. For example, for a bubble initially formed This difference in the rise speeds of bubbles of dif-
at a depth of 5 km beneath the surface, decompres- ferent size is a major factor in bubble coalescence.
sion alone will increase the bubble volume by a However, the absolute rise speeds, and hence the
factor of more than 1000 and hence the bubble relative speeds of bubbles, are much greater in low-
radius by a factor of 10 by the time the bubble viscosity magmas than in melts that are very viscous
reaches the surface. (Table 2.1). Consider a 100 µm diameter bubble ris-
ing through a melt with density ρ = 2500 kg m −3
m
(we can neglect the gas density because it is much
5.5.3 Bubble coalescence
less than this). In a basaltic magma with viscosity
−1
The final process by which bubbles can grow is 30 Pa s this bubble would rise at 1.8 µms whereas
5
through coalescence. This is only a significant pro- in a rhyolitic magma with viscosity 10 Pa s its rise
cess in certain circumstances, but it is important in speed would be more than 3000 times smaller at
−1
transient explosive eruptions such as Strombolian 0.54 nm s . Now consider a bubble that has man-
and Vulcanian eruptions (see Chapter 7). aged to grow to a diameter of 10 mm. This will rise
Bubbles within rising magma are always buoyant at a speed of 18 mm s −1 in the basaltic magma and
−1
compared with the magma due to the low density 5.4 µms in the rhyolite. The ratio of the speeds in
of the gases they contain. This buoyancy means that the two magmas is the same, but the 10 mm bubble