Page 212 - Fundamentals of Probability and Statistics for Engineers

Some Important Continuous Distributions 195
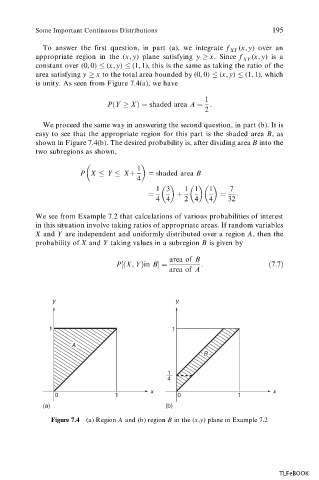
To answer the first question, in part (a), we integrate f XY (x, y) over an
appropriate region in the (x, y) plane satisfying y x. Since f XY (x, y) is a
constant over (0, 0) (x, y) (1, 1), this is the same as taking the ratio of the
area satisfying y x to the total area bounded by (0, 0) (x, y) (1, 1), which
is unity. As seen from Figure 7.4(a), we have
1
P Y X†ˆ shaded area A ˆ :
2

We proceed the same way in answering the second question, in part (b). It is
easy to see that the appropriate region for this part is the shaded area B, as
shown in Figure 7.4(b). The desired probability is, after dividing area B into the
two subregions as shown,

1
PX Y X‡ ˆ shaded area B

4
1 3 1 1 1 7

ˆ ‡ ˆ :
4 4 2 4 4 32
We see from Example 7.2 that calculations of various probabilities of interest
in this situation involve taking ratios of appropriate areas. If random variables
X and Y are independent and uniformly distributed over a region A, then the
probability of X and Y taking values in a subregion B is given by
area of B
P‰ X; Y†in BŠˆ : 7:7†
area of A

y y

1 1

A
B

1
—
4
x x
0 1 0 1
(a) (b)

Figure 7.4 (a) Region A and (b) region B in the (x,y) plane in Example 7.2

TLFeBOOK