Page 213 - Fundamentals of Probability and Statistics for Engineers

196 Fundamentals of Probability and Statistics for Engineers

f XY (x, y) y

1
1
√ 2

x
1

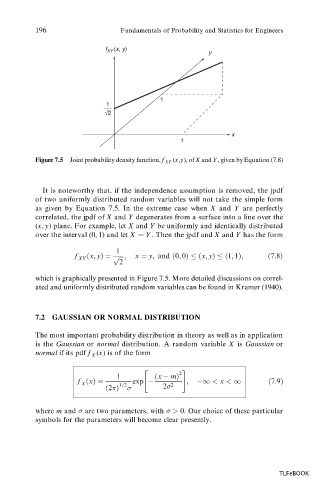
Figure 7.5 Joint probability density function, f XY (x,y), of X and Y, given by Equation (7.8)

It is noteworthy that, if the independence assumption is removed, the jpdf
of two uniformly distributed random variables will not take the simple form
as given by Equation 7.5. In the extreme case when X and Y are perfectly
correlated, the jpdf of X and Y degenerates from a surface into a line over the
(x, y) plane. For example, let X and Y be uniformly and identically distributed
over the interval (0, 1) and let X ˆ Y . Then the jpdf and X and Y has the form

1
f XY x; y†ˆ p ; x ˆ y; and 0; 0† x; y† 1; 1†; 7:8†

2
which is graphically presented in Figure 7.5. More detailed discussions on correl-
ated and uniformly distributed random variables can be found in Kramer (1940).

7.2 GAUSSIAN OR NORMAL DISTRIBUTION

The most important probability distribution in theory as well as in application
is the Gaussian or normal distribution. A random variable X is Gaussian or
normal if its pdf f (x) is of the form
X

" 2 #
1 x m†
f x†ˆ exp ; 1 < x < 1 7:9†
X
2 † 1=2 2 2
where m and are two parameters, with > 0. Our choice of these particular
symbols for the parameters will become clear presently.

TLFeBOOK