Page 320 - Fundamentals of Probability and Statistics for Engineers

Parameter Estimation 303

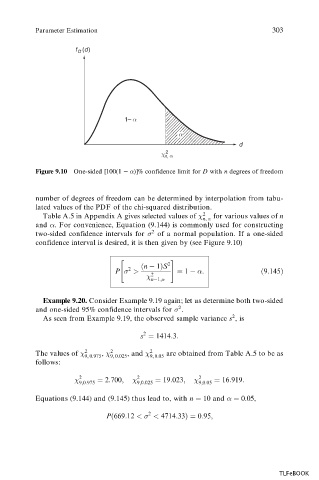
f (d)
D

1– α

α
d
χ n, α
2
Figure 9.10 One-sided [100(1 )]% confidence limit for D with n degrees of freedom

number of degrees of freedom can be determined by interpolation from tabu-
lated values of the PDF of the chi-squared distribution.
Table A.5 in Appendix A gives selected values of 2 n, for various values of n
and . For convenience, Equation (9.144) is commonly used for constructing
two-sided confidence intervals for 2 of a normal population. If a one-sided
confidence interval is desired, it is then given by (see Figure 9.10)

" #
n 1†S 2
2
P > ˆ 1 : 9:145†
2
n 1;
Example 9.20. Consider Example 9.19 again; let us determine both two-sided
and one-sided 95% confidence intervals for 2 .
2
As seen from Example 9.19, the observed sample variance s , is
2
s ˆ 1414:3:
The values of 2 , 2 , and 2 are obtained from Table A.5 to be as
9, 0:975 9, 0:025 9, 0:05
follows:

2 ˆ 2:700; 2 ˆ 19:023; 2 ˆ 16:919:
9;0:975 9;0:025 9;0:05
Equations (9.144) and (9.145) thus lead to, with n ˆ 10 and ˆ 0.05,

2
P 669:12 < < 4714:33†ˆ 0:95;

TLFeBOOK