Page 319 - Fundamentals of Probability and Statistics for Engineers

302 Fundamentals of Probability and Statistics for Engineers

9.3.2.3 Confidence Interval for s 2 in N(m, s 2 )
2
An unbiased point estimator for population variance 2 is S . For the con-
struction of confidence intervals for 2 , let us use the random variable

n 1†S 2
D ˆ ; 9:142†
2
which has been shown in Section 9.1.2 to have a chi-squared distribution with
(n 1) degrees of freedom. Letting 2 n, /2 be the value such that
P D > 2 ) ˆ /2 with n degrees of freedom, we can write (see Figure 9.9)
n, /2
P 2 n 1;1 =2† < D < 2 n 1; =2 †ˆ 1 ; 9:143†

which gives, upon substituting Equation (9.142) for D,

" 2 2 #
n 1†S 2 n 1†S
P < < ˆ 1 : 9:144†
2 2
n 1; =2 n 1;1 =2†
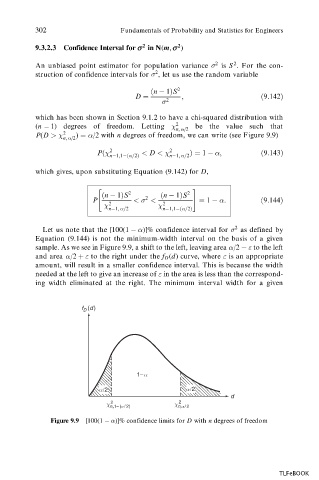
Let us note that the [100(1 )]% confidence interval for 2 as defined by
Equation (9.144) is not the minimum-width interval on the basis of a given
sample. As we see in Figure 9.9, a shift to the left, leaving area /2 " to the left
and area /2 ‡ " to the right under the f D (d) curve, where is an appropriate
"
amount, will result in a smaller confidence interval. This is because the width
"
needed at the left to give an increase of in the area is less than the correspond-
ing width eliminated at the right. The minimum interval width for a given

f (d)
D

1–α

α 2 / α 2 /
d
χ n,1– ( /2) χ α
2
2
α
n, /2
Figure 9.9 [100(1 )]% confidence limits for D with n degrees of freedom

TLFeBOOK