Page 65 - Fundamentals of Probability and Statistics for Engineers

48 Fundamentals of Probability and Statistics for Engineers

p X (x)
f X (x)

1
—
3
1 1
— —
3e
2e 1
—
6e
(a) 3 x (b) 3 x

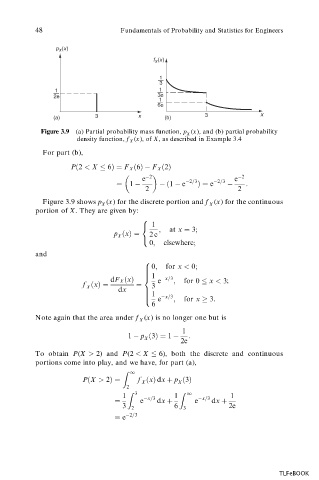
Figure 3.9 (a) Partial probability mass function, p (x), and (b) partial probability

X
density function, f (x), of X, as described in Example 3.4
X
For part (b),
P 2 < X 6†ˆ F X 6† F X 2†
e 2=3 2=3 e
2 2
ˆ 1 1 e †ˆ e :
2 2
Figure 3.9 shows p (x) for the discrete portion and f (x) for the continuous
X X
portion of X. They are given by:
8
1
< ; at x ˆ 3;
p x†ˆ
X 2e
0; elsewhere;
:
and
8
0; for x < 0;
>
>
1
>
dF X x† < e x=3 ; for 0 x < ; 3
>
f x†ˆ ˆ
X 3
dx >
> 1
> x=3
> ; for x 3:
: e
6
Note again that the area under f (x) is no longer one but is
X
1
1 p 3†ˆ 1 :
X
2e
>
To obtain P(X 2) and P(2 X 6), both the discrete and continuous
<
portions come into play, and we have, for part (a),
Z 1
P X > 2†ˆ f x† dx ‡ p 3†
X
X
2
1 Z 3 x=3 1 Z 1 x=3 1
ˆ e dx ‡ e dx ‡
3 2 6 3 2e
ˆ e 2=3
TLFeBOOK