Page 161 - Fundamentals of Radar Signal Processing

(2.120)

For fixed azimuth, this is now a circular convolution of periodic functions
in elevation. Taken together, the two integrals over the angular variables

implement a two-dimensional weighting and averaging over the (θ, ϕ) space. So
long as the antenna beamwidths are small compared to 2π, this circular
convolution will closely approximate a linear convolution in the vicinity of (θ,
ϕ).
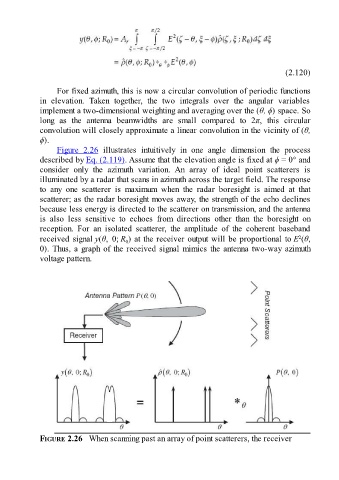
Figure 2.26 illustrates intuitively in one angle dimension the process
described by Eq. (2.119). Assume that the elevation angle is fixed at ϕ = 0° and
consider only the azimuth variation. An array of ideal point scatterers is

illuminated by a radar that scans in azimuth across the target field. The response
to any one scatterer is maximum when the radar boresight is aimed at that
scatterer; as the radar boresight moves away, the strength of the echo declines
because less energy is directed to the scatterer on transmission, and the antenna
is also less sensitive to echoes from directions other than the boresight on
reception. For an isolated scatterer, the amplitude of the coherent baseband

2
received signal y(θ, 0; R ) at the receiver output will be proportional to E (θ,
0
0). Thus, a graph of the received signal mimics the antenna two-way azimuth
voltage pattern.

FIGURE 2.26 When scanning past an array of point scatterers, the receiver