Page 162 - Fundamentals of Radar Signal Processing

output is a superposition of replicas of the antenna pattern.

Assuming a linear receiver so that superposition applies, the response to
two closely spaced point scatterers is proportional to two replicas of the

antenna pattern, overlapped and added to get a composite response. If the two
scatterers are close enough together, the individual responses are not resolved,
but instead blur together into a single peak as illustrated in Fig. 2.26. The details
of the combined response depend on the relative phase of the two individual
responses; they may combine in or out of phase, yielding significantly different

composites. However, the separation at which scatterers are consistently
resolved regardless of relative phase clearly depends on the antenna pattern
2
E (θ, 0), and in particular on the mainlobe beamwidth.
Because of the approximately linear convolution relation of Eq. (2.119) the
spatial Fourier transform of the observed signal is approximately the input
spatial Fourier transform multiplied by the Fourier transform of the antenna
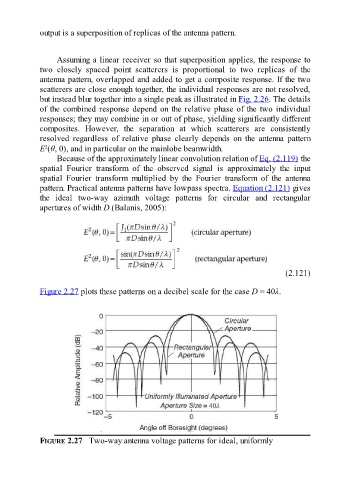
pattern. Practical antenna patterns have lowpass spectra. Equation (2.121) gives

the ideal two-way azimuth voltage patterns for circular and rectangular
apertures of width D (Balanis, 2005):

(2.121)

Figure 2.27 plots these patterns on a decibel scale for the case D = 40λ.

FIGURE 2.27 Two-way antenna voltage patterns for ideal, uniformly