Page 483 - Fundamentals of Radar Signal Processing

declining function only of N.

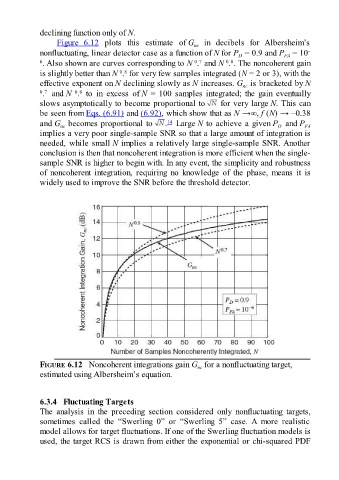
Figure 6.12 plots this estimate of G in decibels for Albersheim’s
nc
nonfluctuating, linear detector case as a function of N for P = 0.9 and P = 10 –
FA
D
6 . Also shown are curves corresponding to N . and N . . The noncoherent gain
0 7
0 8
0 8
is slightly better than N . for very few samples integrated (N = 2 or 3), with the
effective exponent on N declining slowly as N increases. G is bracketed by N
nc
0 7 0 8
. and N . to in excess of N = 100 samples integrated; the gain eventually
slows asymptotically to become proportional to for very large N. This can
be seen from Eqs. (6.91) and (6.92), which show that as N →∞, f (N) → –0.38
14
and G becomes proportional to . Large N to achieve a given P and P FA
nc
D
implies a very poor single-sample SNR so that a large amount of integration is
needed, while small N implies a relatively large single-sample SNR. Another
conclusion is then that noncoherent integration is more efficient when the single-
sample SNR is higher to begin with. In any event, the simplicity and robustness
of noncoherent integration, requiring no knowledge of the phase, means it is
widely used to improve the SNR before the threshold detector.

FIGURE 6.12 Noncoherent integrations gain G for a nonfluctuating target,
nc
estimated using Albersheim’s equation.

6.3.4 Fluctuating Targets

The analysis in the preceding section considered only nonfluctuating targets,
sometimes called the “Swerling 0” or “Swerling 5” case. A more realistic
model allows for target fluctuations. If one of the Swerling fluctuation models is
used, the target RCS is drawn from either the exponential or chi-squared PDF