Page 491 - Fundamentals of Radar Signal Processing

(6.112)

The function sign(x) is +1 if x > 0 and –1 if x < 0. Note that several of the
equations simplify in the nonfluctuating case, K = ∞. Specifically, in this case C 1
= C = 0 so that in turn C = 0 and C = 1.
2
dB
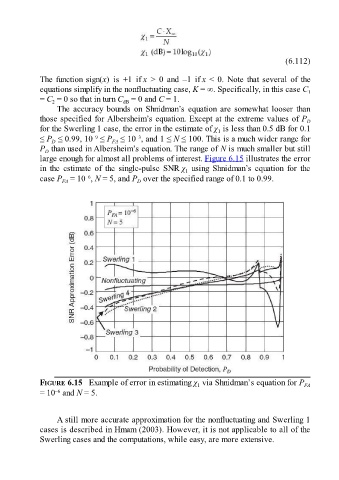
The accuracy bounds on Shnidman’s equation are somewhat looser than
those specified for Albersheim’s equation. Except at the extreme values of P D

for the Swerling 1 case, the error in the estimate of χ is less than 0.5 dB for 0.1
1
–9
–3
≤ P ≤ 0.99, 10 ≤ P ≤ 10 , and 1 ≤ N ≤ 100. This is a much wider range for
D
FA
P than used in Albersheim’s equation. The range of N is much smaller but still
D
large enough for almost all problems of interest. Figure 6.15 illustrates the error
in the estimate of the single-pulse SNR χ using Shnidman’s equation for the
1
–6
case P = 10 , N = 5, and P over the specified range of 0.1 to 0.99.
D
FA

FIGURE 6.15 Example of error in estimating χ via Shnidman’s equation for P FA
1
–6
= 10 and N = 5.

A still more accurate approximation for the nonfluctuating and Swerling 1

cases is described in Hmam (2003). However, it is not applicable to all of the
Swerling cases and the computations, while easy, are more extensive.