Page 255 - Fundamentals of Reservoir Engineering

OILWELL TESTING 192

(t D) in equ. (7.48) can be approximated as ½ In(4 t D /γ) and the last two terms in the
equation will cancel resulting in the simple buildup equation

qB t +∆ t
µ
p = p − 162.2 o log (7.54)
i
ws
kh t ∆
which corresponds to the plot for t ≈ 0 in fig. 7.19.
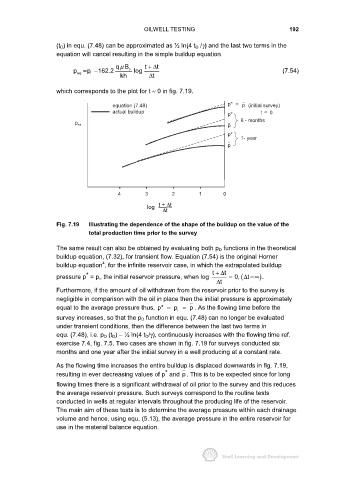
equation (7.48) p* ≈ p (initial survey)
actual buildup p* t ≈ 0
6 - months
p
p ws
p*
1- year
p

4 3 2 1 0

log t + ∆t
∆t
Fig. 7.19 Illustrating the dependence of the shape of the buildup on the value of the
total production time prior to the survey

The same result can also be obtained by evaluating both p D functions in the theoretical
buildup equation, (7.32), for transient flow. Equation (7.54) is the original Horner
4
buildup equation , for the infinite reservoir case, in which the extrapolated buildup
*
pressure p = p i, the initial reservoir pressure, when log t +∆ t = 0, ( t∆ =∞ ).
t ∆
Furthermore, if the amount of oil withdrawn from the reservoir prior to the survey is
negligible in comparison with the oil in place then the initial pressure is approximately
equal to the average pressure thus, p* = p ≈ p . As the flowing time before the
i
survey increases, so that the p D function in equ. (7.48) can no longer be evaluated
under transient conditions, then the difference between the last two terms in
equ. (7.48), i.e. p D (t D) − ½ In(4 t D/γ), continuously increases with the flowing time ref.
exercise 7.4, fig. 7.5. Two cases are shown in fig. 7.19 for surveys conducted six
months and one year after the initial survey in a well producing at a constant rate.

As the flowing time increases the entire buildup is displaced downwards in fig. 7.19,
*
resulting in ever decreasing values of p and p. This is to be expected since for long
flowing times there is a significant withdrawal of oil prior to the survey and this reduces
the average reservoir pressure. Such surveys correspond to the routine tests
conducted in wells at regular intervals throughout the producing life of the reservoir.
The main aim of these tests is to determine the average pressure within each drainage
volume and hence, using equ. (5.13), the average pressure in the entire reservoir for
use in the material balance equation.