Page 190 - gas transport in porous media

184
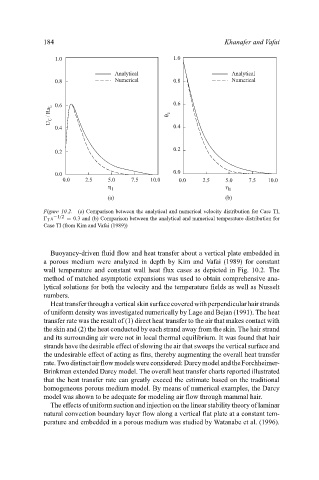
1.0
Analytical 1.0 Khanafer and Vafai
Analytical
0.8 Numerical 0.8 Numerical

U C / Ra L 0.6 θ c 0.6

0.4 0.4

0.2
0.2

0.0
0.0
0.0 2.5 5.0 7.5 10.0 0.0 2.5 5.0 7.5 10.0
η 1 η 1
(a) (b)
Figure 10.2. (a) Comparison between the analytical and numerical velocity distribution for Case TI,
T x −1/2 = 0.3 and (b) Comparison between the analytical and numerical temperature distribution for
Case TI (from Kim and Vafai (1989))

Buoyancy-driven fluid flow and heat transfer about a vertical plate embedded in
a porous medium were analyzed in depth by Kim and Vafai (1989) for constant
wall temperature and constant wall heat flux cases as depicted in Fig. 10.2. The
method of matched asymptotic expansions was used to obtain comprehensive ana-
lytical solutions for both the velocity and the temperature fields as well as Nusselt
numbers.
Heat transfer through a vertical skin surface covered with perpendicular hair strands
of uniform density was investigated numerically by Lage and Bejan (1991). The heat
transfer rate was the result of (1) direct heat transfer to the air that makes contact with
the skin and (2) the heat conducted by each strand away from the skin. The hair strand
and its surrounding air were not in local thermal equilibrium. It was found that hair
strands have the desirable effect of slowing the air that sweeps the vertical surface and
the undesirable effect of acting as fins, thereby augmenting the overall heat transfer
rate. Twodistinctairflowmodelswereconsidered: DarcymodelandtheForchheimer-
Brinkman extended Darcy model. The overall heat transfer charts reported illustrated
that the heat transfer rate can greatly exceed the estimate based on the traditional
homogeneous porous medium model. By means of numerical examples, the Darcy
model was shown to be adequate for modeling air flow through mammal hair.
The effects of uniform suction and injection on the linear stability theory of laminar
natural convection boundary layer flow along a vertical flat plate at a constant tem-
perature and embedded in a porous medium was studied by Watanabe et al. (1996).