Page 67 - gas transport in porous media
P. 67
60
10 10 Webb
10 9 Logarithmic extension
10 8 7
Capillary pressure (Pa) 10 6 5 Original van Genuchten function
(limited data fit)
10
10
10 4
Data
10 3
10 2
0.00 0.20 0.40 0.60 0.80 1.00
Liquid saturation
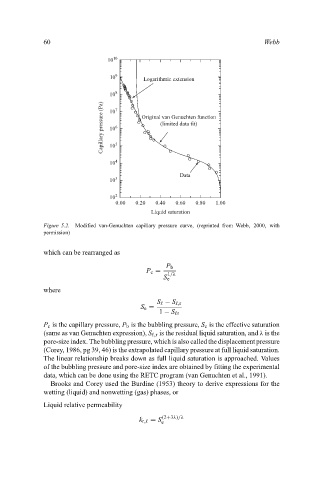
Figure 5.2. Modified van-Genuchten capillary pressure curve, (reprinted from Webb, 2000, with
permission)
which can be rearranged as
P b
P c =
1/λ
S e
where
S − S ,r
S e =
1 − S r
P c is the capillary pressure, P b is the bubbling pressure, S e is the effective saturation
(same as van Genuchten expression), S ,r is the residual liquid saturation, and λ is the
pore-size index. The bubbling pressure, which is also called the displacement pressure
(Corey, 1986, pg 39, 46) is the extrapolated capillary pressure at full liquid saturation.
The linear relationship breaks down as full liquid saturation is approached. Values
of the bubbling pressure and pore-size index are obtained by fitting the experimental
data, which can be done using the RETC program (van Genuchten et al., 1991).
Brooks and Corey used the Burdine (1953) theory to derive expressions for the
wetting (liquid) and nonwetting (gas) phases, or
Liquid relative permeability
k r, = S e (2+3λ)/λ