Page 243 - Geothermal Energy Renewable Energy and The Environment

232 Geothermal Energy: Renewable Energy and the Environment

0
P = pore pressure

5 τ/σ = 0.58
Depth (km)

10 σ 1

15
0 100 200 300 400 500
Stress (MPa)

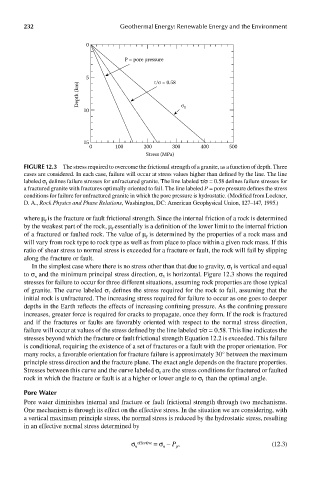
FIGUre 12.3 The stress required to overcome the frictional strength of a granite, as a function of depth. Three
cases are considered. In each case, failure will occur at stress values higher than defined by the line. The line
labeled σ 1 defines failure stresses for unfractured granite. The line labeled τ/σ = 0.58 defines failure stresses for
a fractured granite with fractures optimally oriented to fail. The line labeled P = pore pressure defines the stress
conditions for failure for unfractured granite in which the pore pressure is hydrostatic. (Modified from Lockner,
D. A., Rock Physics and Phase Relations, Washington, DC: American Geophysical Union, 127–147, 1995.)

where μ is the fracture or fault frictional strength. Since the internal friction of a rock is determined
f
by the weakest part of the rock, μ essentially is a definition of the lower limit to the internal friction
f
of a fractured or faulted rock. The value of μ is determined by the properties of a rock mass and
f
will vary from rock type to rock type as well as from place to place within a given rock mass. If this
ratio of shear stress to normal stress is exceeded for a fracture or fault, the rock will fail by slipping
along the fracture or fault.
In the simplest case where there is no stress other than that due to gravity, σ is vertical and equal
1
to σ and the minimum principal stress direction, σ is horizontal. Figure 12.3 shows the required
n
3
stresses for failure to occur for three different situations, assuming rock properties are those typical
of granite. The curve labeled σ defines the stress required for the rock to fail, assuming that the
1
initial rock is unfractured. The increasing stress required for failure to occur as one goes to deeper
depths in the Earth reflects the effects of increasing confining pressure. As the confining pressure
increases, greater force is required for cracks to propagate, once they form. If the rock is fractured
and if the fractures or faults are favorably oriented with respect to the normal stress direction,
failure will occur at values of the stress defined by the line labeled τ/σ = 0.58. This line indicates the
stresses beyond which the fracture or fault frictional strength Equation 12.2 is exceeded. This failure
is conditional, requiring the existence of a set of fractures or a fault with the proper orientation. For
many rocks, a favorable orientation for fracture failure is approximately 30° between the maximum
principle stress direction and the fracture plane. The exact angle depends on the fracture properties.
Stresses between this curve and the curve labeled σ are the stress conditions for fractured or faulted
1
rock in which the fracture or fault is at a higher or lower angle to σ than the optimal angle.
1
pore water
Pore water diminishes internal and fracture or fault frictional strength through two mechanisms.
One mechanism is through its effect on the effective stress. In the situation we are considering, with
a vertical maximum principle stress, the normal stress is reduced by the hydrostatic stress, resulting
in an effective normal stress determined by

σ n effective = σ − P , (12.3)
n
p