Page 295 - Geothermal Energy Systems Exploration, Development, and Utilization

5.6 Bad Urach 271

2
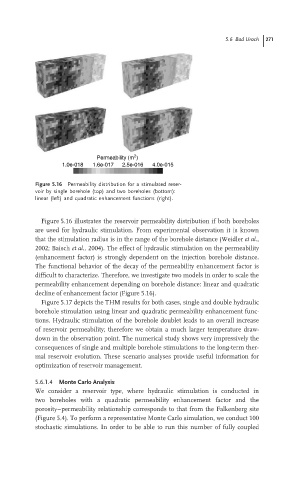
Permeability (m )
1.0e-018 1.6e-017 2.5e-016 4.0e-015

Figure 5.16 Permeability distribution for a stimulated reser-
voir by single borehole (top) and two boreholes (bottom):
linear (left) and quadratic enhancement functions (right).

Figure 5.16 illustrates the reservoir permeability distribution if both boreholes
are used for hydraulic stimulation. From experimental observation it is known
that the stimulation radius is in the range of the borehole distance (Weidler et al.,
2002; Baisch et al., 2004). The effect of hydraulic stimulation on the permeability
(enhancement factor) is strongly dependent on the injection borehole distance.
The functional behavior of the decay of the permeability enhancement factor is
difficult to characterize. Therefore, we investigate two models in order to scale the
permeability enhancement depending on borehole distance: linear and quadratic
decline of enhancement factor (Figure 5.16).
Figure 5.17 depicts the THM results for both cases, single and double hydraulic
borehole stimulation using linear and quadratic permeability enhancement func-
tions. Hydraulic stimulation of the borehole doublet leads to an overall increase
of reservoir permeability; therefore we obtain a much larger temperature draw-
down in the observation point. The numerical study shows very impressively the
consequences of single and multiple borehole stimulations to the long-term ther-
mal reservoir evolution. These scenario analyses provide useful information for
optimization of reservoir management.

5.6.1.4 Monte Carlo Analysis
We consider a reservoir type, where hydraulic stimulation is conducted in
two boreholes with a quadratic permeability enhancement factor and the
porosity–permeability relationship corresponds to that from the Falkenberg site
(Figure 5.4). To perform a representative Monte Carlo simulation, we conduct 100
stochastic simulations. In order to be able to run this number of fully coupled