Page 202 - Global Tectonics
P. 202
188 CHAPTER 7
(a) (c)
t = 370 Myr, Δx = 222 km
0 t = 40 Myr, Δx = 120 km
0
-20 -20
-40 -40 550 C
o
o
-60 550 C -60
-80 -80
o
-100 -100 1000 C
-120 -120
o
1200 C
400 500 600 700 800 400 500 600 700 800
(b)
t = 12 Myr, Δx = 120 km (d)
0 t = 40 Myr, Δx = 120 km
0
-20 -20
o
-40 550 C o
-40 550 C
-60
-60
-80 -80
o
1000 C
o
-100 -100 1000 C
o
-120 1200 C -120
o
1200 C
400 500 600 700 800 400 500 600 700 800 Km
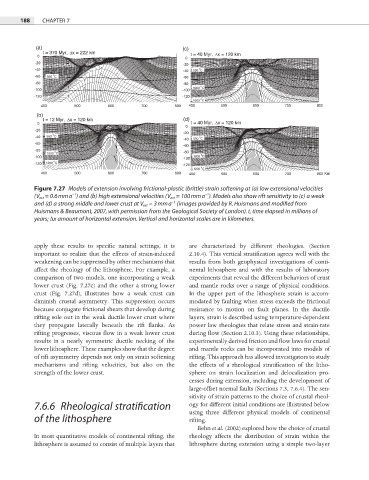
Figure 7.27 Models of extension involving frictional-plastic (brittle) strain softening at (a) low extensional velocities
−1
−1
(V ext = 0.6 mm a ) and (b) high extensional velocities (V ext = 100 mm a ). Models also show rift sensitivity to (c) a weak
−1
and (d) a strong middle and lower crust at V ext = 3 mm a (images provided by R. Huismans and modifi ed from
Huismans & Beaumont, 2007, with permission from the Geological Society of London). t, time elapsed in millions of
years; Δx amount of horizontal extension. Vertical and horizontal scales are in kilometers.
apply these results to specific natural settings, it is are characterized by different rheologies. (Section
important to realize that the effects of strain-induced 2.10.4). This vertical stratification agrees well with the
weakening can be suppressed by other mechanisms that results from both geophysical investigations of conti-
affect the rheology of the lithosphere. For example, a nental lithosphere and with the results of laboratory
comparison of two models, one incorporating a weak experiments that reveal the different behaviors of crust
lower crust (Fig. 7.27c) and the other a strong lower and mantle rocks over a range of physical conditions.
crust (Fig. 7.27d), illustrates how a weak crust can In the upper part of the lithosphere strain is accom-
diminish crustal asymmetry. This suppression occurs modated by faulting when stress exceeds the frictional
because conjugate frictional shears that develop during resistance to motion on fault planes. In the ductile
rifting sole out in the weak ductile lower crust where layers, strain is described using temperature-dependent
they propagate laterally beneath the rift fl anks. As power law rheologies that relate stress and strain-rate
rifting progresses, viscous flow in a weak lower crust during flow (Section 2.10.3). Using these relationships,
results in a nearly symmetric ductile necking of the experimentally derived friction and flow laws for crustal
lower lithosphere. These examples show that the degree and mantle rocks can be incorporated into models of
of rift asymmetry depends not only on strain softening rifting. This approach has allowed investigators to study
mechanisms and rifting velocities, but also on the the effects of a rheological stratification of the litho-
strength of the lower crust. sphere on strain localization and delocalization pro-
cesses during extension, including the development of
large-offset normal faults (Sections 7.3, 7.6.4). The sen-
sitivity of strain patterns to the choice of crustal rheol-
7.6.6 Rheological stratification ogy for different initial conditions are illustrated below
using three different physical models of continental
of the lithosphere rifting.
Behn et al. (2002) explored how the choice of crustal
In most quantitative models of continental rifting, the rheology affects the distribution of strain within the
lithosphere is assumed to consist of multiple layers that lithosphere during extension using a simple two-layer