Page 455 - Handbook of Biomechatronics

The Artificial Pancreas 449

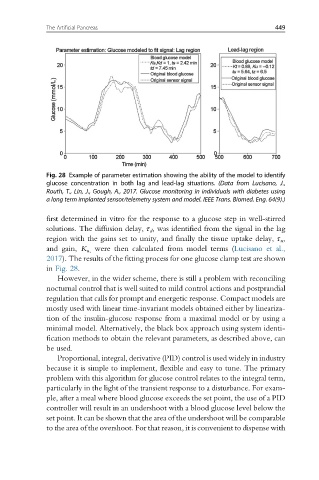
Fig. 28 Example of parameter estimation showing the ability of the model to identify
glucose concentration in both lag and lead-lag situations. (Data from Lucisano, J.,
Routh, T., Lin, J., Gough, A., 2017. Glucose monitoring in individuals with diabetes using
a long term implanted sensor/telemetry system and model. IEEE Trans. Biomed. Eng. 64(9).)

first determined in vitro for the response to a glucose step in well-stirred
solutions. The diffusion delay, τ d , was identified from the signal in the lag
region with the gains set to unity, and finally the tissue uptake delay, τ u ,
and gain, K u, were then calculated from model terms (Lucisano et al.,
2017). The results of the fitting process for one glucose clamp test are shown
in Fig. 28.
However, in the wider scheme, there is still a problem with reconciling
nocturnal control that is well suited to mild control actions and postprandial
regulation that calls for prompt and energetic response. Compact models are
mostly used with linear time-invariant models obtained either by lineariza-
tion of the insulin-glucose response from a maximal model or by using a
minimal model. Alternatively, the black box approach using system identi-
fication methods to obtain the relevant parameters, as described above, can
be used.
Proportional, integral, derivative (PID) control is used widely in industry
because it is simple to implement, flexible and easy to tune. The primary
problem with this algorithm for glucose control relates to the integral term,
particularly in the light of the transient response to a disturbance. For exam-
ple, after a meal where blood glucose exceeds the set point, the use of a PID
controller will result in an undershoot with a blood glucose level below the
set point. It can be shown that the area of the undershoot will be comparable
to the area of the overshoot. For that reason, it is convenient to dispense with