Page 508 - Handbook of Properties of Textile and Technical Fibres

Tensile failure of polyester fibers 481

Stress-strain curves can be parameterized by characteristic points determined by
smoothing and differentiation (Schultze-Gebhardt, 1979; Sujica and Smole, 2003;
Militký and Vaní cek, 1991). It is not necessary to find the approximation function
s(ε), in a closed form, but smoothed (noiseless) data for graphical interpretation,
numerical differentiation, and integration are required. The purpose of numerical
smoothing is to remove the random noise ε i in experimental data and the reconstruc-
tion of noiseless function s(ε). A smoothing function s(ε) must be continuous in the
2
first two derivatives only. Therefore a nonparametric C spline smoothing of the exper-
imental stress-strain curve, determined by the couples s i ; ε i i ¼ 1.N, is useful
2
(Meloun et al., 1994). It has been shown that the function s(ε) from class C , which
minimizes a combination of the smoothness of s(ε) and its closeness to the experi-
mental points, has the following properties:
• The function s(ε) in each interval I j ˛ðε iþ1 ; ε i Þ is a polynomial of at most third degree.
• At all locations ε i , the function s(ε) is a continuous function and in the values of the first two
derivatives.
The full procedure of spline smoothing is described in Meloun et al. (1994). From
the smoothed function s(ε) the shape of the first (modulus E ¼ ds/dε) and second (rate
2
2
modulus D ¼ d s/dε ) derivatives can be simply determined.
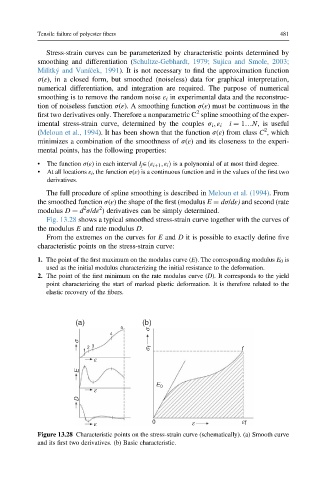
Fig. 13.28 shows a typical smoothed stress-strain curve together with the curves of
the modulus E and rate modulus D.
From the extremes on the curves for E and D it is possible to exactly define five
characteristic points on the stress-strain curve:
1. The point of the first maximum on the modulus curve (E). The corresponding modulus E 0 is
used as the initial modulus characterizing the initial resistance to the deformation.
2. The point of the first minimum on the rate modulus curve (D). It corresponds to the yield
point characterizing the start of marked plastic deformation. It is therefore related to the
elastic recovery of the fibers.

(a) (b)
5 σ
4
σ
2 3
1 σ f f
ε
E

ε E 0
D

ε 0 ε ε f
Figure 13.28 Characteristic points on the stress-strain curve (schematically). (a) Smooth curve
and its first two derivatives. (b) Basic characteristic.