Page 130 - Hardware Implementation of Finite-Field Arithmetic

Operations over GF ( p ) 113

4.6 FPGA Implementations
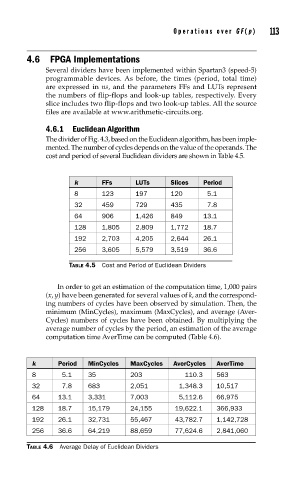
Several dividers have been implemented within Spartan3 (speed-5)
programmable devices. As before, the times (period, total time)
are expressed in ns, and the parameters FFs and LUTs represent
the numbers of flip-flops and look-up tables, respectively. Every
slice includes two flip-flops and two look-up tables. All the source
files are available at www.arithmetic-circuits.org.

4.6.1 Euclidean Algorithm
The divider of Fig. 4.3, based on the Euclidean algorithm, has been imple-
mented. The number of cycles depends on the value of the operands. The
cost and period of several Euclidean dividers are shown in Table 4.5.

k FFs LUTs Slices Period
8 123 197 120 5.1
32 459 729 435 7.8
64 906 1,426 849 13.1
128 1,805 2,809 1,772 18.7
192 2,703 4,205 2,644 26.1
256 3,605 5,579 3,519 36.6

TABLE 4.5 Cost and Period of Euclidean Dividers

In order to get an estimation of the computation time, 1,000 pairs
(x, y) have been generated for several values of k, and the correspond-
ing numbers of cycles have been observed by simulation. Then, the
minimum (MinCycles), maximum (MaxCycles), and average (Aver-
Cycles) numbers of cycles have been obtained. By multiplying the
average number of cycles by the period, an estimation of the average
computation time AverTime can be computed (Table 4.6).

k Period MinCycles MaxCycles AverCycles AverTime
8 5.1 35 203 110.3 563
32 7.8 683 2,051 1,348.3 10,517
64 13.1 3,331 7,003 5,112.6 66,975
128 18.7 15,179 24,155 19,622.1 366,933
192 26.1 32,731 55,467 43,782.7 1,142,728
256 36.6 64,219 88,659 77,624.6 2,841,060

TABLE 4.6 Average Delay of Euclidean Dividers