Page 132 - Hardware Implementation of Finite-Field Arithmetic

Operations over GF ( p ) 115

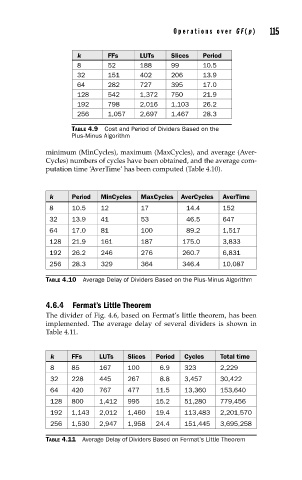
k FFs LUTs Slices Period
8 52 188 99 10.5
32 151 402 206 13.9
64 282 727 395 17.0
128 542 1,372 750 21.9
192 798 2,016 1,103 26.2
256 1,057 2,697 1,467 28.3

TABLE 4.9 Cost and Period of Dividers Based on the
Plus-Minus Algorithm

minimum (MinCycles), maximum (MaxCycles), and average (Aver-
Cycles) numbers of cycles have been obtained, and the average com-
putation time ‘AverTime’ has been computed (Table 4.10).

k Period MinCycles MaxCycles AverCycles AverTime
8 10.5 12 17 14.4 152
32 13.9 41 53 46.5 647
64 17.0 81 100 89.2 1,517
128 21.9 161 187 175.0 3,833
192 26.2 246 276 260.7 6,831
256 28.3 329 364 346.4 10,087
TABLE 4.10 Average Delay of Dividers Based on the Plus-Minus Algorithm

4.6.4 Fermat’s Little Theorem
The divider of Fig. 4.6, based on Fermat’s little theorem, has been
implemented. The average delay of several dividers is shown in
Table 4.11.

k FFs LUTs Slices Period Cycles Total time
8 85 167 100 6.9 323 2,229
32 228 445 267 8.8 3,457 30,422
64 420 767 477 11.5 13,360 153,640
128 800 1,412 995 15.2 51,280 779,456
192 1,143 2,012 1,460 19.4 113,483 2,201,570
256 1,530 2,947 1,958 24.4 151,445 3,695,258

TABLE 4.11 Average Delay of Dividers Based on Fermat’s Little Theorem