Page 209 - Hardware Implementation of Finite-Field Arithmetic

m
Operations over GF (2 )—Polynomial Bases 189

A VHDL model for the classic squaring algorithm (version 2,
Algorithm 7.12) is given in the file classic_squarer.vhd which is
available at www.arithmetic-circuits.org. This model includes the
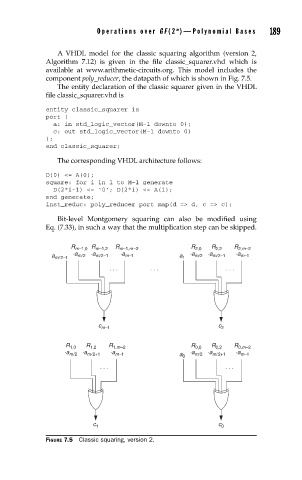
component poly_reducer, the datapath of which is shown in Fig. 7.5.
The entity declaration of the classic squarer given in the VHDL
file classic_squarer.vhd is
entity classic_squarer is
port (
a: in std_logic_vector(M-1 downto 0);
c: out std_logic_vector(M-1 downto 0)
);
end classic_squarer;
The corresponding VHDL architecture follows:

D(0) <= A(0);
square: for i in 1 to M-1 generate
D(2*i-1) <= ‘0’; D(2*i) <= A(i);
end generate;
inst_reduc: poly_reducer port map(d => d, c => c);
Bit-level Montgomery squaring can also be modified using
Eq. (7.33), in such a way that the multiplication step can be skipped.

R m–1,0 R m–1,2 R m–1,m–2 R 2,0 R 2,2 R 2,m–2
a m/ 2–1 ·a m/2 ·a m/2–1 ·a m–1 a 1 ·a m/2 ·a m/2–1 ·a m–1
. . . . . . . . .

c m–1 c 2

R 1,0 R 1,2 R 1,m–2 R 0,0 R 0,2 R 0,m–2
·a m/2 ·a m/ 2+1 ·a m–1 a 0 ·a m/2 ·a m/ 2+1 ·a m–1
. . . . . .

c 1 c 0

FIGURE 7.5 Classic squaring, version 2.