Page 217 - Hardware Implementation of Finite-Field Arithmetic

m
Operations over GF (2 )—Polynomial Bases 197

A (m – 1 : 0)
E (n – 1 : 0) new_c (m – 1 : 0)
1 0 inic

inic ce_c
m-bit register m-bit register
capt
b (m – 1 : 0) c (m – 1 : 0)

start_mul start_sq
Modular Modular
multiplier done_mul squarer done_sq
new_c (m – 1 : 0)
new_b (m – 1 : 0)

start start_mul
start_sq
inic
n-bit shift register State machine
shift_right inic
(control )
ce_c = shift_right
capt = ce_c and e (0)
E (0)
done
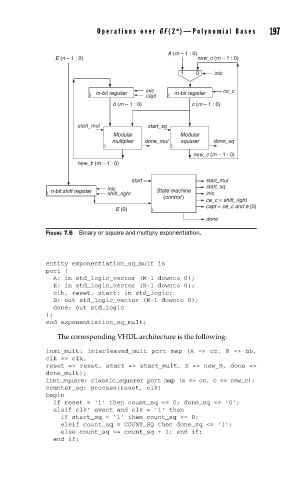
FIGURE 7.6 Binary or square-and-multiply exponentiation.

entity exponentiation_sq_mult is
port (
A: in std_logic_vector (M-1 downto 0);
E: in std_logic_vector (N-1 downto 0);
clk, reset, start: in std_logic;
B: out std_logic_vector (M-1 downto 0);
done: out std_logic
);
end exponentiation_sq_mult;
The corresponding VHDL architecture is the following:

inst_mult: interleaved_mult port map (A => cc, B => bb,
clk => clk,
reset => reset, start => start_mult, Z => new_B, done =>
done_mult);
inst_square: classic_squarer port map (a => cc, c => new_c);
counter_sq: process(reset, clk)
begin
if reset = ‘1’ then count_sq <= 0; done_sq <= ‘0’;
elsif clk’ event and clk = ‘1’ then
if start_sq = ‘1’ then count_sq <= 0;
elsif count_sq = COUNT_SQ then done_sq <= ‘1’;
else count_sq <= count_sq + 1; end if;
end if;