Page 274 - High Power Laser Handbook

242 So l i d - S t at e La s e r s Thin-Disc Lasers 243

16

14
12
Laser power (kW) 10 8 6

4
5 mm pump spot diameter
2 10 mm pump spot diameter
23 mm pump spot diameter
0
0 5 10 15 20 25
Pump power (kW)

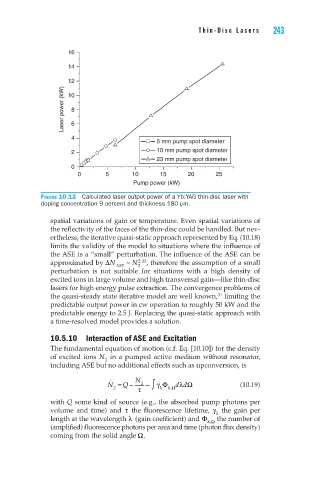
Figure 10.12 Calculated laser output power of a Yb:YAG thin-disc laser with
doping concentration 9 percent and thickness 180 µm.

spatial variations of gain or temperature. Even spatial variations of
the reflectivity of the faces of the thin-disc could be handled. But nev-
ertheless, the iterative quasi-static approach represented by Eq. (10.18)
limits the validity of the model to situations where the influence of
the ASE is a “small” perturbation. The influence of the ASE can be
approximated by DN ASE ~ N 2 2 33 , therefore the assumption of a small
perturbation is not suitable for situations with a high density of
excited ions in large volume and high transversal gain—like thin-disc
lasers for high energy pulse extraction. The convergence problems of
the quasi-steady state iterative model are well known, limiting the
31
predictable output power in cw operation to roughly 50 kW and the
predictable energy to 2.5 J. Replacing the quasi-static approach with
a time-resolved model provides a solution.

10.5.10 Interaction of ASE and Excitation
The fundamental equation of motion (c.f. Eq. [10.10]) for the density
of excited ions N in a pumped active medium without resonator,
2
including ASE but no additional effects such as upconversion, is
N
N = & Q − 2 − ∫ γ ddΩ l Φ (10.19)
2 τ l l , Ω
with Q some kind of source (e.g., the absorbed pump photons per
volume and time) and τ the fluorescence lifetime, γ the gain per
l
length at the wavelength l (gain coefficient) and Φ l, Ω the number of
(amplified) fluorescence photons per area and time (photon flux density)
coming from the solid angle Ω.