Page 152 - How To Solve Word Problems In Calculus

Solution
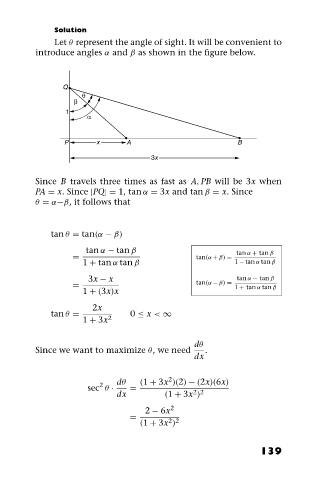
Let θ represent the angle of sight. It will be convenient to
introduce angles α and β as shown in the figure below.

Q
θ
β
1
α

P x A B
3x

Since B travels three times as fast as A, PB will be 3x when
PA = x. Since |PQ|= 1, tan α = 3x and tan β = x. Since
θ = α−β, it follows that

tan θ = tan(α − β)

tan α − tan β tan α + tan β
= tan(α + β) =
1 + tan α tan β 1 − tan α tan β

3x − x tan α − tan β
= tan(α − β) = 1 + tan α tan β
1 + (3x)x
2x
tan θ = 0 ≤ x < ∞
1 + 3x 2

dθ
Since we want to maximize θ, we need .
dx

2
dθ (1 + 3x )(2) − (2x)(6x)
2
sec θ · =
2 2
dx (1 + 3x )
2 − 6x 2
=
2 2
(1 + 3x )
139