Page 157 - How To Solve Word Problems In Calculus
P. 157
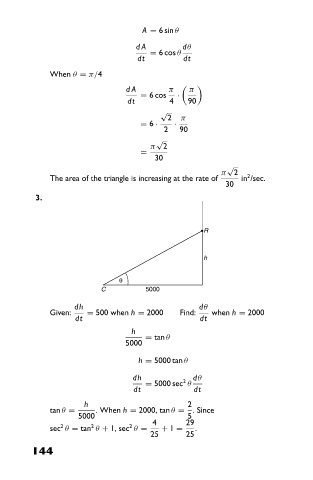
A = 6 sin θ
dA dθ
= 6 cos θ
dt dt
When θ = π/4
dA π π
= 6 cos ·
dt 4 90
√
2 π
= 6 · ·
2 90
√
π 2
=
30
√
π 2
2
The area of the triangle is increasing at the rate of in /sec.
30
3.
R
h
θ
C 5000
dh dθ
Given: = 500 when h = 2000 Find: when h = 2000
dt dt
h
= tan θ
5000
h = 5000 tan θ
dh 2 dθ
= 5000 sec θ
dt dt
h 2
tan θ = . When h = 2000, tan θ = . Since
5000 5
4 29
2 2 2
sec θ = tan θ + 1, sec θ = + 1 = .
25 25
144