Page 256 - Instant notes

Physical chemistry 242

and its repulsion from all other electrons by means of a single equivalent charge at the
center of the atom. For example, Z eff experienced by an electron in the 2s orbital of Li
(Z=3) is 1.26 indicating that the two core electrons do not provide complete screening of
two units of positive charge.
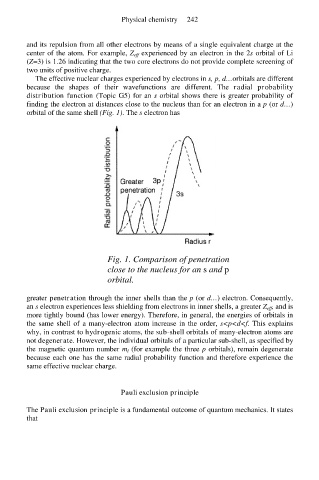
The effective nuclear charges experienced by electrons in s, p, d…orbitals are different
because the shapes of their wavefunctions are different. The radial probability
distribution function (Topic G5) for an s orbital shows there is greater probability of
finding the electron at distances close to the nucleus than for an electron in a p (or d…)
orbital of the same shell (Fig. 1). The s electron has

Fig. 1. Comparison of penetration
close to the nucleus for an s and p
orbital.

greater penetration through the inner shells than the p (or d…) electron. Consequently,
an s electron experiences less shielding from electrons in inner shells, a greater Z eff, and is
more tightly bound (has lower energy). Therefore, in general, the energies of orbitals in
the same shell of a many-electron atom increase in the order, s<p<d<f. This explains
why, in contrast to hydrogenic atoms, the sub-shell orbitals of many-electron atoms are
not degenerate. However, the individual orbitals of a particular sub-shell, as specified by
the magnetic quantum number m l (for example the three p orbitals), remain degenerate
because each one has the same radial probability function and therefore experience the
same effective nuclear charge.

Pauli exclusion principle
The Pauli exclusion principle is a fundamental outcome of quantum mechanics. It states
that