Page 251 - Instant notes

The structure of the hydrogen atom 237

2
2
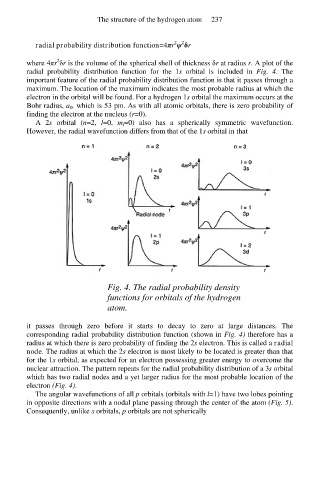
radial probability distribution function=4πr ψ δr
2
where 4πr δr is the volume of the spherical shell of thickness δr at radius r. A plot of the
radial probability distribution function for the 1s orbital is included in Fig. 4. The
important feature of the radial probability distribution function is that it passes through a
maximum. The location of the maximum indicates the most probable radius at which the
electron in the orbital will be found. For a hydrogen 1s orbital the maximum occurs at the
Bohr radius, a 0, which is 53 pm. As with all atomic orbitals, there is zero probability of
finding the electron at the nucleus (r=0).
A 2s orbital (n=2, l=0, m l=0) also has a spherically symmetric wavefunction.
However, the radial wavefunction differs from that of the 1s orbital in that

Fig. 4. The radial probability density
functions for orbitals of the hydrogen
atom.

it passes through zero before it starts to decay to zero at large distances. The
corresponding radial probability distribution function (shown in Fig. 4) therefore has a
radius at which there is zero probability of finding the 2s electron. This is called a radial
node. The radius at which the 2s electron is most likely to be located is greater than that
for the 1s orbital, as expected for an electron possessing greater energy to overcome the
nuclear attraction. The pattern repeats for the radial probability distribution of a 3s orbital
which has two radial nodes and a yet larger radius for the most probable location of the
electron (Fig. 4).
The angular wavefunctions of all p orbitals (orbitals with l=1) have two lobes pointing
in opposite directions with a nodal plane passing through the center of the atom (Fig. 5).
Consequently, unlike s orbitals, p orbitals are not spherically