Page 303 - Instant notes

Strong solid phase interactions 289

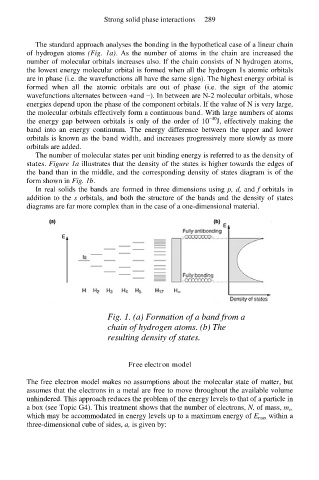
The standard approach analyses the bonding in the hypothetical case of a linear chain
of hydrogen atoms (Fig. 1a). As the number of atoms in the chain are increased the
number of molecular orbitals increases also. If the chain consists of N hydrogen atoms,
the lowest energy molecular orbital is formed when all the hydrogen 1s atomic orbitals
are in phase (i.e. the wavefunctions all have the same sign). The highest energy orbital is
formed when all the atomic orbitals are out of phase (i.e. the sign of the atomic
wavefunctions alternates between +and −). In between are N-2 molecular orbitals, whose
energies depend upon the phase of the component orbitals. If the value of N is very large,
the molecular orbitals effectively form a continuous band. With large numbers of atoms
the energy gap between orbitals is only of the order of 10 −40 J, effectively making the
band into an energy continuum. The energy difference between the upper and lower
orbitals is known as the band width, and increases progressively more slowly as more
orbitals are added.
The number of molecular states per unit binding energy is referred to as the density of
states. Figure 1a illustrates that the density of the states is higher towards the edges of
the band than in the middle, and the corresponding density of states diagram is of the
form shown in Fig. 1b.
In real solids the bands are formed in three dimensions using p, d, and f orbitals in
addition to the s orbitals, and both the structure of the bands and the density of states
diagrams are far more complex than in the case of a one-dimensional material.

Fig. 1. (a) Formation of a band from a
chain of hydrogen atoms. (b) The
resulting density of states.

Free electron model

The free electron model makes no assumptions about the molecular state of matter, but
assumes that the electrons in a metal are free to move throughout the available volume
unhindered. This approach reduces the problem of the energy levels to that of a particle in
a box (see Topic G4). This treatment shows that the number of electrons, N, of mass, m e,
which may be accommodated in energy levels up to a maximum energy of E max within a
three-dimensional cube of sides, a, is given by: