Page 411 - Integrated Wireless Propagation Models

T h e l e e C o m p r e h e n s i v e M o d e l - I n t e g r a t i o n o f t h e T h r e e l e e M o d e l s 389

Water surface

.r:.
'E.
(J)
0

Seabed Seabed
(a) (b)

Water surface Water surface

.r:. .r:.
'E. 'E.
(J) (J)
0 0

Seabed Seabed
(c) (d)
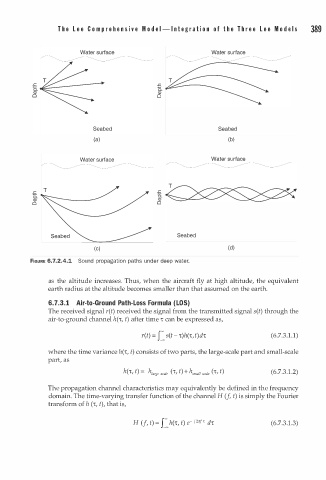
FIGURE 6.7.2.4.1 Sound propagation paths under deep water.

as the altitude increases. Thus, when the aircraft fly at high altitude, the equivalent
earth radius at the altitude becomes smaller than that assumed on the earth.

6.7. . 1 Air-to-Ground Path-Loss Formula L OS)
(
3
The received signal r(t ) received the signal from the transmitted signal s(t ) through the
air-to-ground channel h('t, t ) after time 't can be expressed as,
r(t ) = [ s(t - 't)h('t, t ) d't (6.7.3.1.1)

where the time variance h('t, t ) consists of two parts, the large-scale part and small-scale
part, as
h('t, f) = h la r g e scal e ('t, f) + h small scal e ('t, f) (6.7.3.1.2)

The propagation channel characteristics may equivalently be defined in the frequency
domain. The time-varying transfer function of the channel H (f, t ) is simply the Fourier
transform of h ('t, t ), that is,

(6.7.3.1.3)