Page 258 - Intelligent Digital Oil And Gas Fields

208 Intelligent Digital Oil and Gas Fields

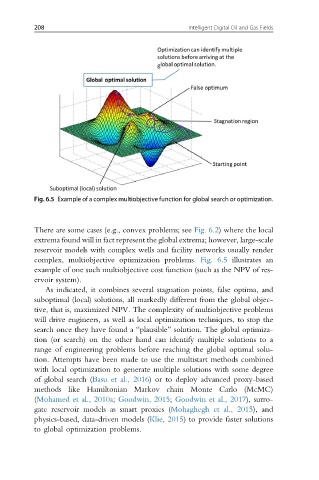
Fig. 6.5 Example of a complex multiobjective function for global search or optimization.

There are some cases (e.g., convex problems; see Fig. 6.2) where the local
extrema found will in fact represent the global extrema; however, large-scale
reservoir models with complex wells and facility networks usually render
complex, multiobjective optimization problems. Fig. 6.5 illustrates an
example of one such multiobjective cost function (such as the NPV of res-
ervoir system).
As indicated, it combines several stagnation points, false optima, and
suboptimal (local) solutions, all markedly different from the global objec-
tive, that is, maximized NPV. The complexity of multiobjective problems
will drive engineers, as well as local optimization techniques, to stop the
search once they have found a “plausible” solution. The global optimiza-
tion (or search) on the other hand can identify multiple solutions to a
range of engineering problems before reaching the global optimal solu-
tion. Attempts have been made to use the multistart methods combined
with local optimization to generate multiple solutions with some degree
of global search (Basu et al., 2016) or to deploy advanced proxy-based
methods like Hamiltonian Markov chain Monte Carlo (McMC)
(Mohamed et al., 2010a; Goodwin, 2015; Goodwin et al., 2017), surro-
gate reservoir models as smart proxies (Mohaghegh et al., 2015), and
physics-based, data-driven models (Klie, 2015) to provide faster solutions
to global optimization problems.