Page 81 - Intro to Tensor Calculus

76

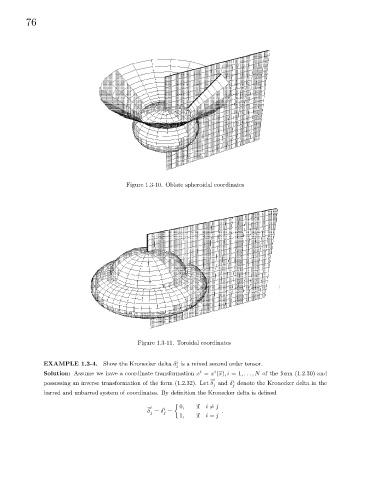
Figure 1.3-10. Oblate spheroidal coordinates

Figure 1.3-11. Toroidal coordinates

i
EXAMPLE 1.3-4. Show the Kronecker delta δ is a mixed second order tensor.
j
i
i
Solution: Assume we have a coordinate transformation x = x (x),i =1,... ,N of the form (1.2.30) and
i
i
possessing an inverse transformation of the form (1.2.32). Let δ and δ denote the Kronecker delta in the
j j
barred and unbarred system of coordinates. By definition the Kronecker delta is defined

i i 0, if i 6= j
δ = δ = .
j
j
1, if i = j