Page 190 - Introduction to Information Optics

3.2. Light Propagation in Optical Fibers 1 O
propagating along the fiber that corresponds to m = 0. Substituting m = 0 into
the above equation, we get

2
2
ft • J'o a] V/F-- n\kl • K'^ft - n\k\ a) '
This equation can be further simplified by using the identity relationship of
Bessel functions; i.e., J' 0(x) = J,(x) and K' 0(x) = K^(x). Then, we get

(3.34)
2
J,(v/n?fc§ - ft a] tiffi • K
V
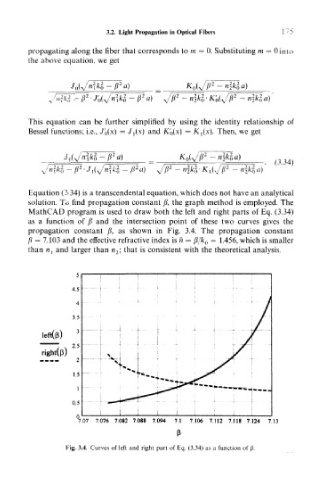
Equation (3.34) is a transcendental equation, which does not have an analytical
solution. To find propagation constant /?, the graph method is employed. The
MathCAD program is used to draw both the left and right parts of Eq. (3.34)
as a function of /i and the intersection point of these two curves gives the
propagation constant /?, as shown in Fig. 3.4. The propagation constant
/i = 7.103 and the effective refractive index is h = /?//c 0 = 1.456, which is smaller
than «j and larger than n 2; that is consistent with the theoretical analysis.

5
4,5
4
3.5

3
2.5
right(p)
2
1.5

1
0.5

7.07 7.076 7.082 7.088 7.094 7.1 7.106 7.112 7.118 7.124 7.13

Fig. 3.4. Curves of left and right part of Eq. (3.34) as a function of