Page 303 - Introduction to Information Optics

288 5. Transformation with Optics

(a) (b)
2
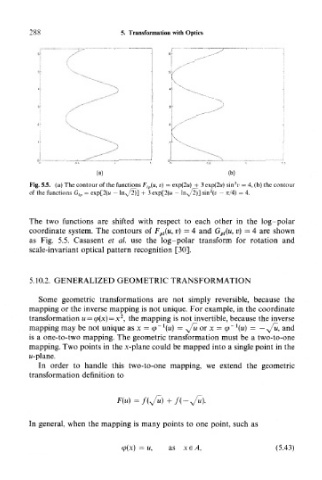
Fig. 5.5. (a) The contour of the functions F lp(u, v) = exp(2u) + 3 exp(2w) sin v — 4, (b) the contour
2
of the functions G lp = exp[2(u - ln v/2)] + 3 exp[2(n - ln x/2)] sin (p - n/4) = 4.

The two functions are shifted with respect to each other in the log -polar
coordinate system. The contours of F pl(u, v) = 4 and G pl(u, v) = 4 are shown
as Fig. 5.5. Casasent et al. use the log-polar transform for rotation and
scale-invariant optical pattern recognition [30].

5.10.2. GENERALIZED GEOMETRIC TRANSFORMATION

Some geometric transformations are not simply reversible, because the
mapping or the inverse mapping is not unique. For example, in the coordinate
2
transformation u = <p(x) = x , the mapping is not invertible, because the inverse
l
mapping may be not unique as x = cp (u) — ^/u or x = <p (u) — — *ju, and
is a one-to-two mapping. The geometric transformation must be a two-to-one
mapping. Two points in the x-plane could be mapped into a single point in the
w-plane.
In order to handle this two-to-one mapping, we extend the geometric
transformation definition to

In general, when the mapping is many points to one point, such as

(p(x) — u, as xeA, (5.43)