Page 122 - Introduction to chemical reaction engineering and kinetics

104 Chapter 5: Complex Systems

For reaction in a constant-volume BR, with only A present initially, the concentra-
tions of A, B and C as functions of time t are governed by the following material-
balance equations for A, B and C, respectively, incorporating the two independent rate
laws:

-dc,ldt = klcA (5.5-2)

dcnldt = klcA - k2cB

CC = CA0 - CA - CB (5.5-4)

The first two equations can be integrated to obtain CA(t) and c*(t) in turn, and the
results used in the third to obtain c&t). Anticipating the quantitative results, we can
deduce the general features of these functions from the forms of the equations above.
The first involves only A, and is the same for A decomposing by a first-order process
to B, since A has no direct “knowledge” of C. Thus, the CA(t) profile is an exponential
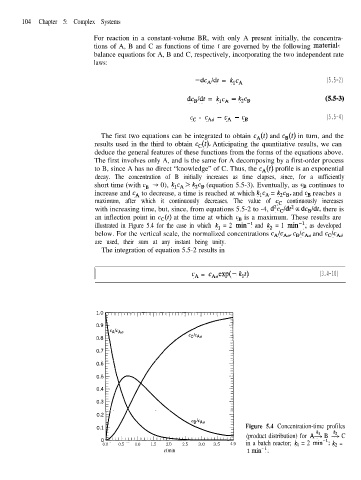
decay. The concentration of B initially increases as time elapses, since, for a sufficiently
short time (with cn -+ 0), k,c, > k2cB (equation 5.5-3). Eventually, as cn continues to
increase and CA to decrease, a time is reached at which k,c, = k2cB, and cn reaches a
maximum, after which it continuously decreases. The value of cc continuously increases
with increasing time, but, since, from equations 5.5-2 to -4, d2c,ldt2 cc dc,/dt, there is
an inflection point in c&t) at the time at which cB is a maximum. These results are
illustrated in Figure 5.4 for the case in which kl = 2 min-l and k2 = 1 min-‘, as developed

below. For the vertical scale, the normalized concentrations cAIcA~, cBIcA~ and cC/CA~
are used, their sum at any instant being unity.
The integration of equation 5.5-2 results in

CA = C&Xp(- k,t) (3.4-10) )

Figure 5.4 Concentration-time profiles
(product distribution) for AA B 2 C
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 in a batch reactor; kl = 2 min-‘; k2 =
1 rnin-‘.