Page 38 - Introduction to chemical reaction engineering and kinetics

20 Chapter 1: Introduction

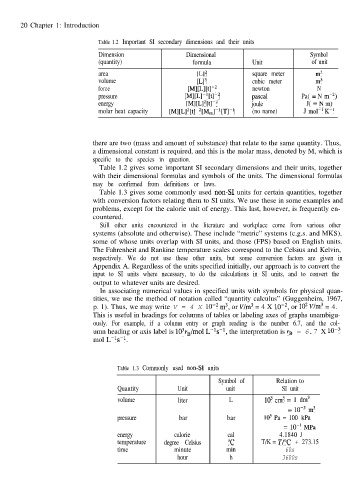
Table 1.2 Important SI secondary dimensions and their units
Dimension Dimensional Symbol
(quantity) formula Unit of unit

area 1L12 square meter m2
volume [L13 cubic meter m3
force MMtl-* newton N
pressure M[W1[tl-2 Pascal Pa( = N mm*)
energy [Ml[L12[tl-2 joule J( -Nm)
molar heat capacity ~~1~~12~~1-2~~~1-‘~~1-1 (no name) J mol-’ K-l

there are two (mass and amount of substance) that relate to the same quantity. Thus,
a dimensional constant is required, and this is the molar mass, denoted by M, which is
specific to the species in question.
Table 1.2 gives some important SI secondary dimensions and their units, together
with their dimensional formulas and symbols of the units. The dimensional formulas
may be confirmed from definitions or laws.
Table 1.3 gives some commonly used non-S1 units for certain quantities, together
with conversion factors relating them to SI units. We use these in some examples and
problems, except for the calorie unit of energy. This last, however, is frequently en-
countered.
Still other units encountered in the literature and workplace come from various other
systems (absolute and otherwise). These include “metric” systems (c.g.s. and MKS),
some of whose units overlap with SI units, and those (FPS) based on English units.
The Fahrenheit and Rankine temperature scales correspond to the Celsius and Kelvin,
respectively. We do not use these other units, but some conversion factors are given in
Appendix A. Regardless of the units specified initially, our approach is to convert the
input to SI units where necessary, to do the calculations in SI units, and to convert the
output to whatever units are desired.
In associating numerical values in specified units with symbols for physical quan-
tities, we use the method of notation called “quantity calculus” (Guggenheim, 1967,
p. 1). Thus, we may write V = 4 X 10e2 m3, or V/m3 = 4 X 10m2, or lo2 V/m3 = 4.
This is useful in headings for columns of tables or labeling axes of graphs unambigu-
ously. For example, if a column entry or graph reading is the number 6.7, and the col-
umn heading or axis label is 103rnlmol L-%-i, the interpretation is r, = 6.7 X 10e3
mol L-ls-l.

Table 1.3 Commonly used non-S1 units

Symbol of Relation to
Quantity Unit unit SI unit
volume liter L lo3 cm3 = 1 dm3
= 10m3 m3
pressure bar bar lo5 Pa = 100 kPa
= lo-’ MPa
energy calorie cal 4.1840 J
temperature degree Celsius “C T/K = TPC + 273.15
time minute min 60s
hour h 3600s