Page 57 - Lindens Handbook of Batteries

2.14 PRINCIPLES OF OPERATION

Electrode
surface Outer Helmholtz plane φ o

+
+
+
Potential + +

+
+
Inner Helmholtz plane φ i

Distance
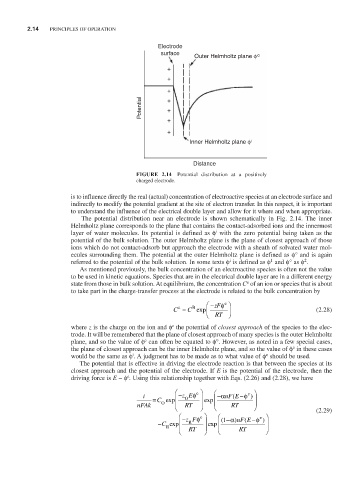
FIGURE 2.14 Potential distribution at a positively
charged electrode.

is to influence directly the real (actual) concentration of electroactive species at an electrode surface and
indirectly to modify the potential gradient at the site of electron transfer. In this respect, it is important
to understand the influence of the electrical double layer and allow for it where and when appropriate.
The potential distribution near an electrode is shown schematically in Fig. 2.14. The inner
Helmholtz plane corresponds to the plane that contains the contact-adsorbed ions and the innermost
i
layer of water molecules. Its potential is defined as φ with the zero potential being taken as the
potential of the bulk solution. The outer Helmholtz plane is the plane of closest approach of those
ions which do not contact-adsorb but approach the electrode with a sheath of solvated water mol-
ecules surrounding them. The potential at the outer Helmholtz plane is defined as φ° and is again
1
2
i
referred to the potential of the bulk solution. In some texts φ is defined as φ and φ° as φ .
As mentioned previously, the bulk concentration of an electroactive species is often not the value
to be used in kinetic equations. Species that are in the electrical double layer are in a different energy
e
state from those in bulk solution. At equilibrium, the concentration C of an ion or species that is about
to take part in the charge-transfer process at the electrode is related to the bulk concentration by
 - zFφ e 
e
B
C = C exp   RT   (2.28)
e
where z is the charge on the ion and φ the potential of closest approach of the species to the elec-
trode. It will be remembered that the plane of closest approach of many species is the outer Helmholtz
e
plane, and so the value of φ can often be equated to φ°. However, as noted in a few special cases,
e
the plane of closest approach can be the inner Helmholtz plane, and so the value of φ in these cases
e
i
would be the same as φ . A judgment has to be made as to what value of φ should be used.
The potential that is effective in driving the electrode reaction is that between the species at its
closest approach and the potential of the electrode. If E is the potential of the electrode, then the
e
driving force is E - φ . Using this relationship together with Eqs. (2.26) and (2.28), we have
 e   
i = C exp  - zEφ  exp  - nF E-α ( φ e ) 
O
nFAk O   RT     RT   
(2.29)
 -zFφ e   - )α nnF E( -φ e 
-C exp  R  exp  (1 ) 
R  RT   RT 
   