Page 133 - Marine Structural Design
P. 133
Chapter 6 mshore Structural Analysis 109
where, d), is any values, the stifhess matrix equation for an element is
{de [KI, {4, (6.10)
=
where, is a stiffhess matrix
[KI, = 6 [BIT EZbb
=I/[ 412 -61 :ill (6.11)
‘QI’
61 -12 61
13 -12 -61 12
61 212 -61 412
6.3.3 Stiffness Matrix for 3D Beam Elements
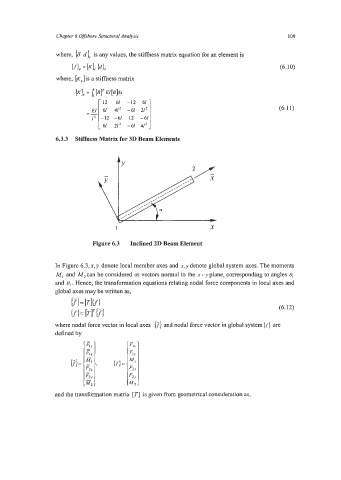
Figure 6.3 Inclined 2D Beam Element
In Figure 6.3, x.7 denote local member axes and X,JJ denote global system axes. The moments
M, and M, can be considered as vectors normal to the x - y plane, corresponding to angles e,
and B2. Hence, the transformation equations relating nodal force components in local axes and
global axes may be written as,
(6.12)
-
FL’ 61’
-
4Y - FIY
M, MI
’
{TI= F,, ’7 dr) = F2x
-
F2Y - F2Y
.M2, .M2,
and the transformation matrix [TI is given from geometrical consideration as,