Page 282 - Marks Calculation for Machine Design

P1: Shibu
January 4, 2005
14:56
Brown.cls
Brown˙C06
STRENGTH OF MACHINES
264
s
A
cr
Parabolic formula
Critical stress S y C
S /2 D Euler formula
y
B
(L/k) C (L/k) D
Slenderness ratio (L/k)
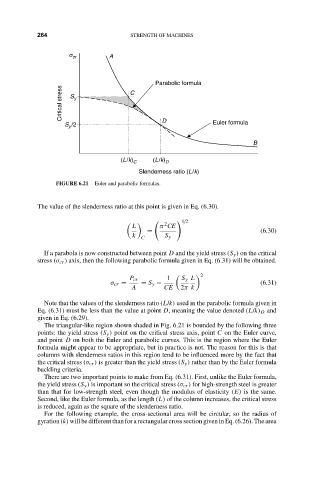
FIGURE 6.21 Euler and parabolic formulas.

The value of the slenderness ratio at this point is given in Eq. (6.30).

1/2
L π CE
2
= (6.30)
k C S y
If a parabola is now constructed between point D and the yield stress (S y ) on the critical
stress (σ cr ) axis, then the following parabolic formula given in Eq. (6.31) will be obtained.

P cr 1 S y L 2
σ cr = = S y − (6.31)
A CE 2π k
Note that the values of the slenderness ratio (L/k) used in the parabolic formula given in
Eq. (6.31) must be less than the value at point D, meaning the value denoted (L/k) D and
given in Eq. (6.29).
The triangular-like region shown shaded in Fig. 6.21 is bounded by the following three
points: the yield stress (S y ) point on the critical stress axis, point C on the Euler curve,
and point D on both the Euler and parabolic curves. This is the region where the Euler
formula might appear to be appropriate, but in practice is not. The reason for this is that
columns with slenderness ratios in this region tend to be influenced more by the fact that
the critical stress (σ cr ) is greater than the yield stress (S y ) rather than by the Euler formula
buckling criteria.
There are two important points to make from Eq. (6.31). First, unlike the Euler formula,
the yield stress (S y ) is important so the critical stress (σ cr ) for high-strength steel is greater
than that for low-strength steel, even though the modulus of elasticity (E) is the same.
Second, like the Euler formula, as the length (L) of the column increases, the critical stress
is reduced, again as the square of the slenderness ratio.
For the following example, the cross-sectional area will be circular, so the radius of
gyration (k) will be different than for a rectangular cross section given in Eq. (6.26). The area