Page 285 - Marks Calculation for Machine Design

P1: Shibu
January 4, 2005
14:56
Brown.cls
Brown˙C06
STATIC DESIGN AND COLUMN BUCKLING
where e = eccentricity
c = maximum distance from the neutral axis to farthest point in cross section 267
ec
= eccentricity ratio
k 2
The other terms in Eq. (6.34) are as already defined. Note the secant function in the
denominator; that is where its name is derived from. (The secant function is the inverse of the
cosinefunction,soatzerothesecantis1,andthenbecomesverylargeasitapproaches[π/2].)
The secant formula in Eq. (6.34) cannot be solved explicitly for the critical stress (σ cr ).
Either a trial-and-error method or numerical methods are suggested in most references.
Actually, the trial-and-error method is easy to employ, at least to an accuracy needed in the
design of a machine element, so there is no need to be intimidated by the prospects of doing
numerical methods.
The mathematical nature of the secant formula means that if a particular material is
regularly used for a class of columns, then to avoid repetitive trial-and-error solutions a
2
set of design curves for various values of the eccentricity ratio ec/k is recommended, like
those shown in Fig. 6.22.
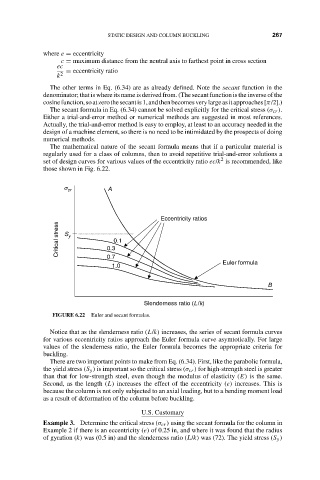
s cr A
Eccentricity ratios
Critical stress S y 0.3 0.1

0.7
Euler formula
1.0
B

Slenderness ratio (L/k)
FIGURE 6.22 Euler and secant formulas.

Notice that as the slenderness ratio (L/k) increases, the series of secant formula curves
for various eccentricity ratios approach the Euler formula curve asymtotically. For large
values of the slenderness ratio, the Euler formula becomes the appropriate criteria for
buckling.
There are two important points to make from Eq. (6.34). First, like the parabolic formula,
the yield stress (S y ) is important so the critical stress (σ cr ) for high-strength steel is greater
than that for low-strength steel, even though the modulus of elasticity (E) is the same.
Second, as the length (L) increases the effect of the eccentricity (e) increases. This is
because the column is not only subjected to an axial loading, but to a bending moment load
as a result of deformation of the column before buckling.

U.S. Customary
Example 3. Determine the critical stress (σ cr ) using the secant formula for the column in
Example 2 if there is an eccentricity (e) of 0.25 in, and where it was found that the radius
of gyration (k) was (0.5 in) and the slenderness ratio (L/k) was (72). The yield stress (S y )