Page 208 - Master Handbook of Acoustics

Wallace Clement Sabine, a Harvard University physics professor, devised the first reverberation-
time equation. He used a portable wind chest and organ pipes as a sound source, a stopwatch, and
keen ears to measure the time from the interruption of the source to inaudibility. Today we have better
technical measuring facilities, but we can only refine our understanding of the basic concept. The

equation used to calculate reverberation time, often called the Sabine equation, is presented in the
next section.
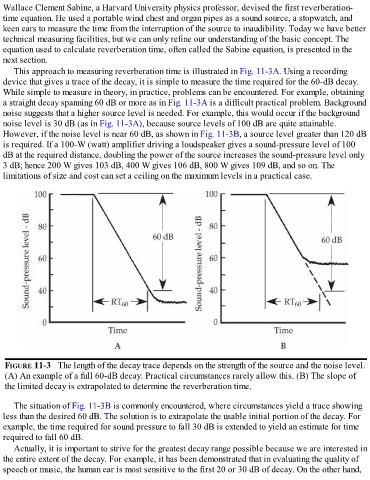
This approach to measuring reverberation time is illustrated in Fig. 11-3A. Using a recording
device that gives a trace of the decay, it is simple to measure the time required for the 60-dB decay.
While simple to measure in theory, in practice, problems can be encountered. For example, obtaining
a straight decay spanning 60 dB or more as in Fig. 11-3A is a difficult practical problem. Background

noise suggests that a higher source level is needed. For example, this would occur if the background
noise level is 30 dB (as in Fig. 11-3A), because source levels of 100 dB are quite attainable.
However, if the noise level is near 60 dB, as shown in Fig. 11-3B, a source level greater than 120 dB
is required. If a 100-W (watt) amplifier driving a loudspeaker gives a sound-pressure level of 100
dB at the required distance, doubling the power of the source increases the sound-pressure level only
3 dB; hence 200 W gives 103 dB, 400 W gives 106 dB, 800 W gives 109 dB, and so on. The

limitations of size and cost can set a ceiling on the maximum levels in a practical case.

FIGURE 11-3 The length of the decay trace depends on the strength of the source and the noise level.
(A) An example of a full 60-dB decay. Practical circumstances rarely allow this. (B) The slope of
the limited decay is extrapolated to determine the reverberation time.

The situation of Fig. 11-3B is commonly encountered, where circumstances yield a trace showing
less than the desired 60 dB. The solution is to extrapolate the usable initial portion of the decay. For
example, the time required for sound pressure to fall 30 dB is extended to yield an estimate for time

required to fall 60 dB.
Actually, it is important to strive for the greatest decay range possible because we are interested in
the entire extent of the decay. For example, it has been demonstrated that in evaluating the quality of
speech or music, the human ear is most sensitive to the first 20 or 30 dB of decay. On the other hand,