Page 128 - Mathematical Models and Algorithms for Power System Optimization

118 Chapter 4

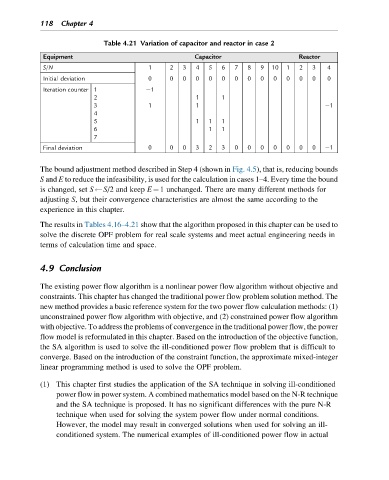
Table 4.21 Variation of capacitor and reactor in case 2
Equipment Capacitor Reactor
S/N 1 2 3 4 5 6 7 8 9 10 1 2 3 4

Initial deviation 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Iteration counter 1 1
2 1 1
3 1 1 1
4
5 1 1 1
6 1 1
7
0 0 0 3 2 3 0 0 0 0 0 0 0 1
Final deviation
The bound adjustment method described in Step 4 (shown in Fig. 4.5), that is, reducing bounds
S and E to reduce the infeasibility, is used for the calculation in cases 1–4. Every time the bound
is changed, set S S/2 and keep E¼1 unchanged. There are many different methods for
adjusting S, but their convergence characteristics are almost the same according to the
experience in this chapter.
The results in Tables 4.16–4.21 show that the algorithm proposed in this chapter can be used to
solve the discrete OPF problem for real scale systems and meet actual engineering needs in
terms of calculation time and space.

4.9 Conclusion

The existing power flow algorithm is a nonlinear power flow algorithm without objective and
constraints. This chapter has changed the traditional power flow problem solution method. The
new method provides a basic reference system for the two power flow calculation methods: (1)
unconstrained power flow algorithm with objective, and (2) constrained power flow algorithm
with objective. To address the problems of convergence in the traditional power flow, the power
flow model is reformulated in this chapter. Based on the introduction of the objective function,
the SA algorithm is used to solve the ill-conditioned power flow problem that is difficult to
converge. Based on the introduction of the constraint function, the approximate mixed-integer
linear programming method is used to solve the OPF problem.

(1) This chapter first studies the application of the SA technique in solving ill-conditioned
power flow in power system. A combined mathematics model based on the N-R technique
and the SA technique is proposed. It has no significant differences with the pure N-R
technique when used for solving the system power flow under normal conditions.
However, the model may result in converged solutions when used for solving an ill-
conditioned system. The numerical examples of ill-conditioned power flow in actual