Page 215 - Mathematical Models and Algorithms for Power System Optimization

206 Chapter 6

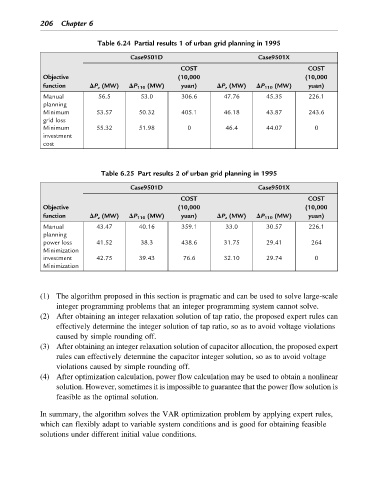
Table 6.24 Partial results 1 of urban grid planning in 1995

Case9501D Case9501X
COST COST
Objective (10,000 (10,000
function ΔP z (MW) ΔP 110 (MW) yuan) ΔP z (MW) ΔP 110 (MW) yuan)

Manual 56.5 53.0 306.6 47.76 45.35 226.1
planning
Minimum 53.57 50.32 405.1 46.18 43.87 243.6
grid loss
Minimum 55.32 51.98 0 46.4 44.07 0
investment
cost

Table 6.25 Part results 2 of urban grid planning in 1995
Case9501D Case9501X
COST COST
Objective (10,000 (10,000
function ΔP z (MW) ΔP 110 (MW) yuan) ΔP z (MW) ΔP 110 (MW) yuan)

Manual 43.47 40.16 359.1 33.0 30.57 226.1
planning
power loss 41.52 38.3 438.6 31.75 29.41 264
Minimization
investment 42.75 39.43 76.6 32.10 29.74 0
Minimization

(1) The algorithm proposed in this section is pragmatic and can be used to solve large-scale
integer programming problems that an integer programming system cannot solve.
(2) After obtaining an integer relaxation solution of tap ratio, the proposed expert rules can
effectively determine the integer solution of tap ratio, so as to avoid voltage violations
caused by simple rounding off.
(3) After obtaining an integer relaxation solution of capacitor allocation, the proposed expert
rules can effectively determine the capacitor integer solution, so as to avoid voltage
violations caused by simple rounding off.
(4) After optimization calculation, power flow calculation may be used to obtain a nonlinear
solution. However, sometimes it is impossible to guarantee that the power flow solution is
feasible as the optimal solution.

In summary, the algorithm solves the VAR optimization problem by applying expert rules,
which can flexibly adapt to variable system conditions and is good for obtaining feasible
solutions under different initial value conditions.