Page 214 - Mathematical Models and Algorithms for Power System Optimization

Discrete Optimization for Reactive Power Planning 205

Table 6.22 Optimization results of investment costs and reactive compensation

Investment Costs VAR Installation
Optimal
Initial Value Value
(10,000 (10,000 Descending Initial Value Optimal Descending
Case Name yuan) yuan) Rate (%) (Mvar) Value (Mvar) Rate (%)
951D 306.6 0.0 100 233.8 174.8 25.2
951X 226.1 0.0 100 183.0 66.8 63.5
952D 359.1 75.6 78.9 286.4 223.8 21.9
952X 226.1 0.0 100 183.0 98.6 46.1
Table 6.23 Optimization results of VAR installation nodes

Initial Installation Nodes Optimized Installation Nodes Descending
Rate After
Case Original Original New Original Original New Optimization
Name Nodes +New Nodes Total Nodes +New Nodes Total (%)

951D 30 10 19 59 33 0 0 33 44.1
951X 12 9 12 33 14 0 0 14 57.6
952D 27 10 21 58 33 4 2 39 32.8
952X 14 7 14 35 14 0 0 14 60.0

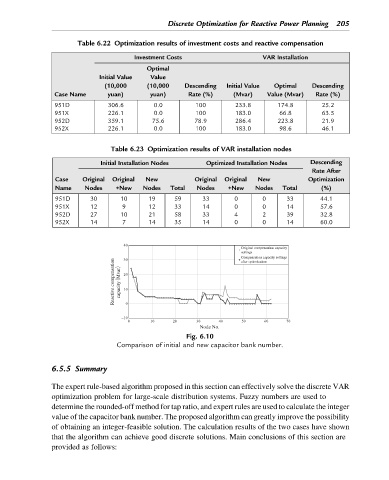
Original compensation capacity
settings
Compensation capacity settings
Reactive compensation ʢMvarʣ capacity
after optimization

Node No.
Fig. 6.10
Comparison of initial and new capacitor bank number.

6.5.5 Summary

The expert rule-based algorithm proposed in this section can effectively solve the discrete VAR
optimization problem for large-scale distribution systems. Fuzzy numbers are used to
determine the rounded-off method for tap ratio, and expert rules are used to calculate the integer
value of the capacitor bank number. The proposed algorithm can greatly improve the possibility
of obtaining an integer-feasible solution. The calculation results of the two cases have shown
that the algorithm can achieve good discrete solutions. Main conclusions of this section are
provided as follows: