Page 89 - Mathematical Models and Algorithms for Power System Optimization

Optimization of Annual Generator Maintenance Scheduling 79

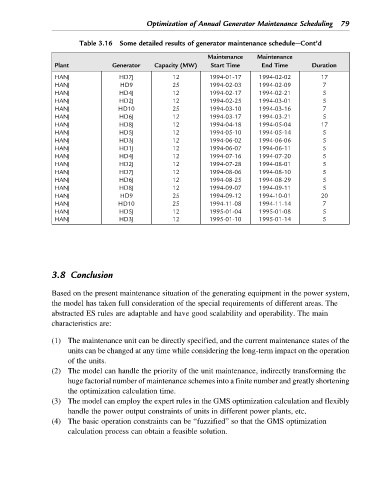
Table 3.16 Some detailed results of generator maintenance schedule—Cont’d
Maintenance Maintenance
Plant Generator Capacity (MW) Start Time End Time Duration

HANJ HD7J 12 1994-01-17 1994-02-02 17
HANJ HD9 25 1994-02-03 1994-02-09 7
HANJ HD4J 12 1994-02-17 1994-02-21 5
HANJ HD2J 12 1994-02-25 1994-03-01 5
HANJ HD10 25 1994-03-10 1994-03-16 7
HANJ HD6J 12 1994-03-17 1994-03-21 5
HANJ HD8J 12 1994-04-18 1994-05-04 17
HANJ HD5J 12 1994-05-10 1994-05-14 5
HANJ HD3J 12 1994-06-02 1994-06-06 5
HANJ HD1J 12 1994-06-07 1994-06-11 5
HANJ HD4J 12 1994-07-16 1994-07-20 5
HANJ HD2J 12 1994-07-28 1994-08-01 5
HANJ HD7J 12 1994-08-06 1994-08-10 5
HANJ HD6J 12 1994-08-25 1994-08-29 5
HANJ HD8J 12 1994-09-07 1994-09-11 5
HANJ HD9 25 1994-09-12 1994-10-01 20
HANJ HD10 25 1994-11-08 1994-11-14 7
HANJ HD5J 12 1995-01-04 1995-01-08 5
HANJ HD3J 12 1995-01-10 1995-01-14 5

3.8 Conclusion

Based on the present maintenance situation of the generating equipment in the power system,
the model has taken full consideration of the special requirements of different areas. The
abstracted ES rules are adaptable and have good scalability and operability. The main
characteristics are:
(1) The maintenance unit can be directly specified, and the current maintenance states of the
units can be changed at any time while considering the long-term impact on the operation
of the units.
(2) The model can handle the priority of the unit maintenance, indirectly transforming the
huge factorial number of maintenance schemes into a finite number and greatly shortening
the optimization calculation time.
(3) The model can employ the expert rules in the GMS optimization calculation and flexibly
handle the power output constraints of units in different power plants, etc.
(4) The basic operation constraints can be “fuzzified” so that the GMS optimization
calculation process can obtain a feasible solution.