Page 312 - Mathematical Techniques of Fractional Order Systems

Sliding Mode Stabilization and Synchronization Chapter | 10 301

(A) 40

30
20

Error (1) 10 0

–10
–20

–30
0 0.5 1 1.5 2 2.5 3
Time (s)
(B)
40
30

20

Error (1) 10 0

–10

–20
–30
0 0.5 1 1.5 2 2.5 3
Time (s)
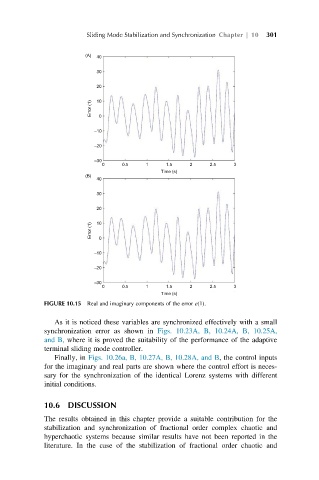
FIGURE 10.15 Real and imaginary components of the error e(1).

As it is noticed these variables are synchronized effectively with a small
synchronization error as shown in Figs. 10.23A, B, 10.24A, B, 10.25A,
and B, where it is proved the suitability of the performance of the adaptive
terminal sliding mode controller.
Finally, in Figs. 10.26a, B, 10.27A, B, 10.28A, and B, the control inputs
for the imaginary and real parts are shown where the control effort is neces-
sary for the synchronization of the identical Lorenz systems with different
initial conditions.

10.6 DISCUSSION
The results obtained in this chapter provide a suitable contribution for the
stabilization and synchronization of fractional order complex chaotic and
hyperchaotic systems because similar results have not been reported in the
literature. In the case of the stabilization of fractional order chaotic and