Page 42 - Mathematical Techniques of Fractional Order Systems

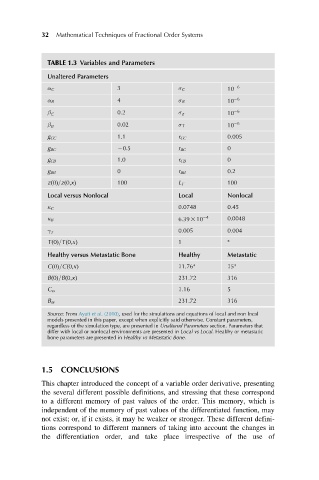
32 Mathematical Techniques of Fractional Order Systems

TABLE 1.3 Variables and Parameters
Unaltered Parameters

α C 3 σ C 10 26
α B 4 σ B 10 26
0.2 26
β C σ z 10
β B 0.02 σ T 10 26
g CC 1.1 r CC 0.005
g BC 20:5 r BC 0
g CB 1.0 r CB 0
g BB 0 r BB 0.2
zð0Þ=zð0;xÞ 100 L T 100
Local versus Nonlocal Local Nonlocal

κ C 0.0748 0.45
κ B 6:39 3 10 24 0:0048
0.005 0.004
γ T
Tð0Þ=Tð0;xÞ 1
Healthy versus Metastatic Bone Healthy Metastatic
Cð0Þ=Cð0;xÞ 11.76 15
Bð0Þ=Bð0;xÞ 231.72 316
C ss 1.16 5
B ss 231.72 316
Source: From Ayati et al. (2010), used for the simulations and equations of local and non local
models presented in this paper, except when explicitly said otherwise. Constant parameters,
regardless of the simulation type, are presented in Unaltered Parameters section. Parameters that
differ with local or nonlocal environments are presented in Local vs Local. Healthy or metastatic
bone parameters are presented in Healthy vs Metastatic Bone.

1.5 CONCLUSIONS
This chapter introduced the concept of a variable order derivative, presenting
the several different possible definitions, and stressing that these correspond
to a different memory of past values of the order. This memory, which is
independent of the memory of past values of the differentiated function, may
not exist; or, if it exists, it may be weaker or stronger. These different defini-
tions correspond to different manners of taking into account the changes in
the differentiation order, and take place irrespective of the use of